题目内容
(理)已知数列{an},对于任意的正整数n,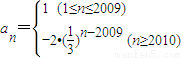 ,设Sn表示数列{an}的前n项和.下列关于
,设Sn表示数列{an}的前n项和.下列关于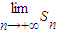 的结论,正确的是( )
的结论,正确的是( )A.
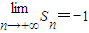
B.
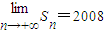
C.
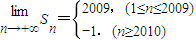 (n∈N*)
(n∈N*)D.以上结论都不对
【答案】分析:由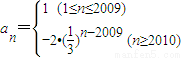 ,知a1=a2=a3=…=a2009=1,
,知a1=a2=a3=…=a2009=1,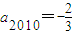 ,
,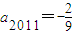 ,
, ,…所以
,…所以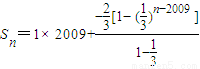 =
=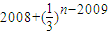 ,由此能求出
,由此能求出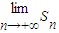 .
.
解答:解:∵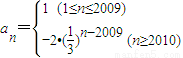 ,
,
∴a1=a2=a3=…=a2009=1,
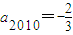 ,
,
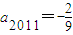 ,
,
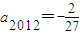 ,
,
…
∴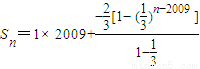
=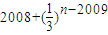 ,
,
∴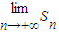 =
=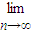
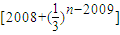
=2008.
故选B.
点评:本题考查数列的极限的求法,解题时要认真审题,注意挖掘题设中的隐含条件,解题的关键是正确求出Sn.
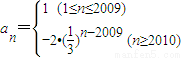 ,知a1=a2=a3=…=a2009=1,
,知a1=a2=a3=…=a2009=1,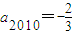 ,
,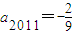 ,
, ,…所以
,…所以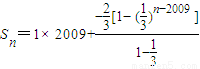 =
=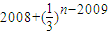 ,由此能求出
,由此能求出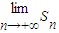 .
.解答:解:∵
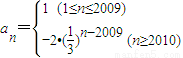 ,
,∴a1=a2=a3=…=a2009=1,
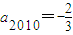 ,
,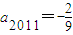 ,
,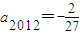 ,
,…
∴
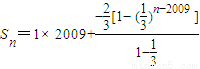
=
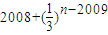 ,
,∴
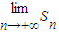 =
=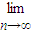
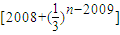
=2008.
故选B.
点评:本题考查数列的极限的求法,解题时要认真审题,注意挖掘题设中的隐含条件,解题的关键是正确求出Sn.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目