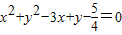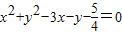题目内容
以(1,1)和(2,-2)为一条直径的两个端点的圆的方程是( )
分析:由已知的两点为直径的两端点,可得连接两点的线段的中点为圆心,连接两点线段长度的一半为圆的半径,故由中点坐标公式求出两点的中点,即为圆心坐标,利用两点间的距离公式求出两点间的距离,求出距离的一半即为圆的半径,根据求出的圆心坐标和半径写出圆的方程即可.
解答:解:∵(1,1)和(2,-2)为一条直径的两个端点,
∴两点的中点(
,
)即(
,-
)为圆的圆心,
又两点间的距离d=
=
,
∴圆的半径为
,
则所求圆的方程为(x-
)2+(y+
)2=
,即x2+y2-3x+y=0.
故选D
∴两点的中点(
| 1+2 |
| 2 |
| 1-2 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
又两点间的距离d=
| (1-2)2+(1+2)2 |
| 10 |
∴圆的半径为
| ||
| 2 |
则所求圆的方程为(x-
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
故选D
点评:此题考查了圆的标准方程,涉及的知识有:中点坐标公式,两点间的距离公式,以及圆标准方程与一般式方程的转化,其中根据题意求出圆心坐标和圆的半径是解本题的关键.

练习册系列答案
相关题目