题目内容
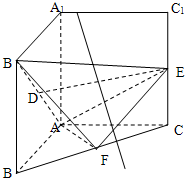 (2012•平遥县模拟)把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点.
(2012•平遥县模拟)把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点.(1)求证:DE∥平面ABC;
(2)求证:B1F⊥平面AEF;
(3)求二面角A-EB1-F的大小.
分析:(1)取AB的中点为G,连接DG,CG;根据条件可以得到CEDG是平行四边形即可得到结论;
(2)直接把问题转化为证明AF⊥B1F以及B1F⊥EF;
(3)先建立空间直角坐标系,求出两个半平面的法向量,再代入向量的夹角计算公式即可.
(2)直接把问题转化为证明AF⊥B1F以及B1F⊥EF;
(3)先建立空间直角坐标系,求出两个半平面的法向量,再代入向量的夹角计算公式即可.
解答: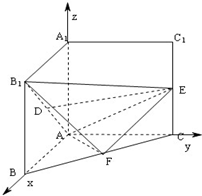 (本小题满分12分)
(本小题满分12分)
解:(1)设AB的中点为G,连接DG,CG
∵D是A1B的中点
∴DG∥A1A且DG=
A1A…(2分)
∵E是C1C的中点
∴CE∥A1A且CE=
A1A,
∴CE∥DG且CE=DG
∴CEDG是平行四边形,
∴DE∥GC
∵DE?平面ABC,GC?平面ABC,
∴DE∥平面ABC…(4分)
(2)∵△ABC为等腰直角三角形,∠BAC=90°,且F是BC的中点
∴AF⊥BC
∵平面ABC⊥平面BCC1B1
∴AF⊥平面BCC1B1
∴AF⊥B1F…(6分)
设AB=AA1=2,则在B1FE中,B1F=
,
则EF=
,B1E=3
∴B1E2=B1F2+EF2=9
∴△B1FE是直角三角形,
∴B1F⊥EF
∵AF∩EF=F
∴B1F⊥平面AEF…(8分)
(3)分别以AB,AC,AA1为x,y,z轴建立空间直角
坐标系A-xyz如图,
设AB=AA1=2,则
设A(0,0,0),B1(2,0,2),E(0,2,1),F(1,1,0),D(1,0,1)…(9分)
∵AF⊥平面BCC1B1,
∴面B1FE的法向量为
=(1,1,0),…(10分)
设平面AB1E的法向量为
=(x,y,z),
∵
=(0,2,1),
=(1,0,1)
∴
•
=0,
•
=0,
∴2y+z=0,,x+z=0,
不妨设z=-2,可得
=(2,1,-2)…(11分)
∴cos<
,
>=
=
=
∵二面角A-EB1-F是锐角,
∴二面角A-EB1-F的大小45°…(12分)
 (本小题满分12分)
(本小题满分12分)解:(1)设AB的中点为G,连接DG,CG
∵D是A1B的中点
∴DG∥A1A且DG=
| 1 |
| 2 |
∵E是C1C的中点
∴CE∥A1A且CE=
| 1 |
| 2 |
∴CE∥DG且CE=DG
∴CEDG是平行四边形,
∴DE∥GC
∵DE?平面ABC,GC?平面ABC,
∴DE∥平面ABC…(4分)
(2)∵△ABC为等腰直角三角形,∠BAC=90°,且F是BC的中点
∴AF⊥BC
∵平面ABC⊥平面BCC1B1
∴AF⊥平面BCC1B1
∴AF⊥B1F…(6分)
设AB=AA1=2,则在B1FE中,B1F=
| 6 |
则EF=
| 3 |
∴B1E2=B1F2+EF2=9
∴△B1FE是直角三角形,
∴B1F⊥EF
∵AF∩EF=F
∴B1F⊥平面AEF…(8分)
(3)分别以AB,AC,AA1为x,y,z轴建立空间直角
坐标系A-xyz如图,
设AB=AA1=2,则
设A(0,0,0),B1(2,0,2),E(0,2,1),F(1,1,0),D(1,0,1)…(9分)
∵AF⊥平面BCC1B1,
∴面B1FE的法向量为
| AF |
设平面AB1E的法向量为
| n |
∵
| AE |
| AD |
∴
| AE |
| n |
| AD |
| n |
∴2y+z=0,,x+z=0,
不妨设z=-2,可得
| n |
∴cos<
| n |
| AF |
| ||||
|
|
| 3 | ||
3
|
| ||
| 2 |
∵二面角A-EB1-F是锐角,
∴二面角A-EB1-F的大小45°…(12分)
点评:本题第三问主要考查利用空间向量知识求二面角,解决问题的关键是建立适当的坐标系,并准确求出两个半平面的法向量.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
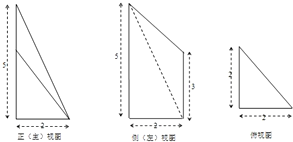 (2012•平遥县模拟)一个几何体的三视图如图所示,则这个几何体的体积等于
(2012•平遥县模拟)一个几何体的三视图如图所示,则这个几何体的体积等于