题目内容
(2012•平遥县模拟)已知函数f(x)=x2+alnx
(Ⅰ)当a=-2时,求函数f(x)的单调区间;
(Ⅱ)若g(x)=f(x)+
在[1,+∞)上是单调函数,求实数a的取值范围.
(Ⅰ)当a=-2时,求函数f(x)的单调区间;
(Ⅱ)若g(x)=f(x)+
| 2 | x |
分析:(Ⅰ)求导函数,利用导数的正负,可得函数的单调递增区间与单调递减区间;
(Ⅱ)由题意得g'(x)=2x+
-
,分函数g(x)为[1,+∞)上的单调增函数与单调减函数讨论,即可确定实数a的取值范围.
(Ⅱ)由题意得g'(x)=2x+
| a |
| x |
| 2 |
| x2 |
解答:解:(Ⅰ)求导函数可得f′(x)=2x-
=
(x>0)
令f′(x)>0,则-1<x<0或x>1,∵x>0,∴x>1;
令f′(x)<0,则x<-1或0<x<1,∵x>0,∴0<x<1;
∴函数的单调递增区间是(1,+∞),单调递减区间是(0,1).
(Ⅱ)由题意得g'(x)=2x+
-
,
①若函数g(x)为[1,+∞)上的单调增函数,则2x+
-
≥0在[1,+∞)上恒成立,即a≥
-2x2 在[1,+∞)上恒成立,
设Φ(x)=
-2x2,∵Φ(x)在[1,+∞)上单调递减,
∴Φ(x)≤Φ(1)=0,∴a≥0
②若函数g(x)为[1,+∞)上的单调减函数,则 g'(x)≤0在[1,+∞)上恒成立,不可能.
∴实数a的取值范围[0,+∞)
| 2 |
| x |
| 2(x+1)(x-1) |
| x |
令f′(x)>0,则-1<x<0或x>1,∵x>0,∴x>1;
令f′(x)<0,则x<-1或0<x<1,∵x>0,∴0<x<1;
∴函数的单调递增区间是(1,+∞),单调递减区间是(0,1).
(Ⅱ)由题意得g'(x)=2x+
| a |
| x |
| 2 |
| x2 |
①若函数g(x)为[1,+∞)上的单调增函数,则2x+
| a |
| x |
| 2 |
| x2 |
| 2 |
| x |
设Φ(x)=
| 2 |
| x |
∴Φ(x)≤Φ(1)=0,∴a≥0
②若函数g(x)为[1,+∞)上的单调减函数,则 g'(x)≤0在[1,+∞)上恒成立,不可能.
∴实数a的取值范围[0,+∞)
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,正确运用分离参数法是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
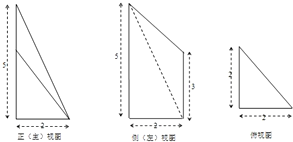 (2012•平遥县模拟)一个几何体的三视图如图所示,则这个几何体的体积等于
(2012•平遥县模拟)一个几何体的三视图如图所示,则这个几何体的体积等于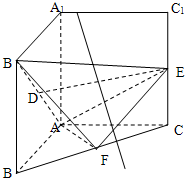 (2012•平遥县模拟)把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点.
(2012•平遥县模拟)把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点.