题目内容
已知函数f(x)=alnx-ax-3(a∈R).(Ⅰ) 若a>0,求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的斜率是1,问:m在什么范围取值时,对于任意的t∈[1,2],函数g(x)=x3+x2[
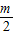 +f′(x)]在区间(t,3)上总存在极值?
+f′(x)]在区间(t,3)上总存在极值?
【答案】分析:(1)利用导数求函数的单调区间的步骤是①求导函数f′(x);②解f′(x)>0(或<0);③得到函数的增区间(或减区间),
(2)点(2,f(2))处的切线的斜率为1,即f'(2)=1,可求a值,代入得g(x)的解析式,由t∈[1,2],且g(x)在区间(t,3)上总不是单调函数可知: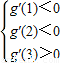 ,于是可求m的范围.
,于是可求m的范围.
解答:解:(Ⅰ)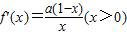 ,
,
当a>0时,f(x)的单调增区间为(0,1],减区间为[1,+∞);
(Ⅱ)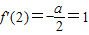 得a=-2,f(x)=-2lnx+2x-3
得a=-2,f(x)=-2lnx+2x-3
∴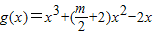 ,
,
∴g'(x)=3x2+(m+4)x-2
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2
∴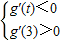 ,
,
由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
所以有: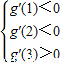 ,∴
,∴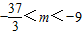 .
.
∴当m∈(-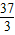 ,-9)内取值时对于任意的t∈[1,2],函数g(x)=x3+x2[
,-9)内取值时对于任意的t∈[1,2],函数g(x)=x3+x2[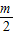 +f′(x)]在区间(t,3)上总存在极值.
+f′(x)]在区间(t,3)上总存在极值.
点评:本题考查利用函数的导数来求函数的单调区间,以及已知函数曲线上一点求曲线的切线方程,考查求导公式的掌握情况,含参数的数学问题的处理,构造函数求解证明不等式问题,属于难题.
(2)点(2,f(2))处的切线的斜率为1,即f'(2)=1,可求a值,代入得g(x)的解析式,由t∈[1,2],且g(x)在区间(t,3)上总不是单调函数可知:
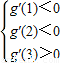 ,于是可求m的范围.
,于是可求m的范围.解答:解:(Ⅰ)
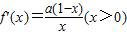 ,
,当a>0时,f(x)的单调增区间为(0,1],减区间为[1,+∞);
(Ⅱ)
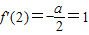 得a=-2,f(x)=-2lnx+2x-3
得a=-2,f(x)=-2lnx+2x-3∴
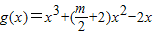 ,
,∴g'(x)=3x2+(m+4)x-2
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2
∴
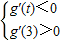 ,
,由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
所以有:
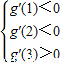 ,∴
,∴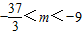 .
.∴当m∈(-
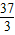 ,-9)内取值时对于任意的t∈[1,2],函数g(x)=x3+x2[
,-9)内取值时对于任意的t∈[1,2],函数g(x)=x3+x2[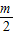 +f′(x)]在区间(t,3)上总存在极值.
+f′(x)]在区间(t,3)上总存在极值.点评:本题考查利用函数的导数来求函数的单调区间,以及已知函数曲线上一点求曲线的切线方程,考查求导公式的掌握情况,含参数的数学问题的处理,构造函数求解证明不等式问题,属于难题.

练习册系列答案
相关题目