题目内容
3.设点P(x,y)是曲线a|x|+b|y|=1(a≥0,b≥0)上任意一点,其坐标(x,y)均满足$\sqrt{{x^2}+{y^2}+2x+1}+\sqrt{{x^2}+{y^2}-2x+1}≤2\sqrt{2}$,则$\sqrt{2}$a+b取值范围为( )| A. | (0,2] | B. | [1,2] | C. | [1,+∞) | D. | [2,+∞) |
分析 曲线a|x|+b|y|=1(a≥0,b≥0),对x,y分类讨论.画出图象:表示菱形ABCD.由$\sqrt{{x^2}+{y^2}+2x+1}+\sqrt{{x^2}+{y^2}-2x+1}≤2\sqrt{2}$,即$\sqrt{(x+1)^{2}+{y}^{2}}$+$\sqrt{(x-1)^{2}+{y}^{2}}$$≤2\sqrt{2}$.设M(-1,0),N(1,0),可得:2|PM|≤2$\sqrt{2}$,|BD|≤2$\sqrt{2}$,解出即可.
解答 解:曲线a|x|+b|y|=1(a≥0,b≥0),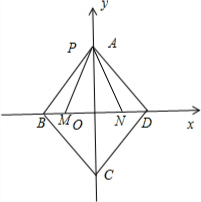
当x,y≥0时,化为ax+by=1;当x≥0,y≤0时,化为ax-by=1;当x≤0,y≥0时,化为-ax+by=1;当x≤0,y≤0时,
化为-ax-by=1.画出图象:表示菱形ABCD.
由$\sqrt{{x^2}+{y^2}+2x+1}+\sqrt{{x^2}+{y^2}-2x+1}≤2\sqrt{2}$,
即$\sqrt{(x+1)^{2}+{y}^{2}}$+$\sqrt{(x-1)^{2}+{y}^{2}}$$≤2\sqrt{2}$.
设M(-1,0),N(1,0),
则2|PM|≤2$\sqrt{2}$,|BD|≤2$\sqrt{2}$,
∴$\sqrt{1+\frac{1}{{b}^{2}}}$$≤\sqrt{2}$,$\frac{2}{a}$$≤2\sqrt{2}$,
解得b≥1,$\sqrt{2}a≥1$,
∴$\sqrt{2}$a+b≥1+1=2.
∴$\sqrt{2}$a+b取值范围为[2,+∞).
故选:D.
点评 本题考查了直线方程、分类讨论思想方法、两点之间的距离公式,考查了数形结合思想方法,考查了推理能力与计算能力,属于难题.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
| A. | 最小值$\frac{1}{27}$ | B. | 最大值$\frac{1}{27}$ | C. | 最小值$\frac{1}{3}$ | D. | 最大值$\frac{1}{3}$ |
| A. | 将函数f(x)=cos(2x+$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位长度可得到g(x)=sin2x的图象 | |
| B. | 将函数f(x)=cos(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{6}$个单位长度可得到g(x)=sin2x的图象 | |
| C. | 将函数g(x)=sin2x的图象向右平移$\frac{5π}{12}$个单位长度可得到f(x)=cos(2x+$\frac{π}{3}$)的图象 | |
| D. | 将函数g(x)=sin2x的图象向左平移$\frac{5π}{12}$个单位长度可得到f(x)=cos(2x+$\frac{π}{3}$)的图象 |
