题目内容
8.若0<x<$\frac{1}{2}$,则x2(1-2x)有( )| A. | 最小值$\frac{1}{27}$ | B. | 最大值$\frac{1}{27}$ | C. | 最小值$\frac{1}{3}$ | D. | 最大值$\frac{1}{3}$ |
分析 记f(x)=x2(1-2x),求其导函数,讨论0<x<$\frac{1}{2}$时,函数f(x)的单调性即可.
解答 解:记f(x)=x2(1-2x)=-2x3+x2,
则f′(x)=-6x2+2x=-2x(3x-1),
令f′(x)=0,则x=0或$\frac{1}{3}$,
显然当$0<x<\frac{1}{3}$时,f(x)单调递增,当$\frac{1}{3}<x<\frac{1}{2}$时,f(x)单调递减,
故当0<x<$\frac{1}{2}$时,函数f(x)有最大值:$f(\frac{1}{3})$=$(\frac{1}{3})^{2}×(1-2×\frac{1}{3})$=$\frac{1}{27}$,
故选:B.
点评 本题考查利用导数求单调性,进而求最值,属于基础题.

练习册系列答案
相关题目
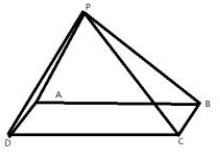 如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD.