题目内容
已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点B1在底面上的射影D落在BC上,
(1)求证:AC⊥平面BB1C1C;
(2)若AB1⊥BC1,D为BC的中点,求α;
(3)若α=arccos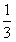 ,AC=BC=AA1时,求二面角C1-AB-C的大小。
,AC=BC=AA1时,求二面角C1-AB-C的大小。
(1)求证:AC⊥平面BB1C1C;
(2)若AB1⊥BC1,D为BC的中点,求α;
(3)若α=arccos
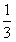 ,AC=BC=AA1时,求二面角C1-AB-C的大小。
,AC=BC=AA1时,求二面角C1-AB-C的大小。 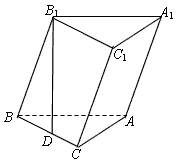
解:(1)∵B1D⊥平面ABC,AC 平面ABC,
平面ABC,
∴B1D⊥AC,
又AC⊥BC,BC∩B1D=D,
∴AC⊥平面BB1C1C;
(2)∵AC⊥平面BB1C1C,AB1⊥BC1,
由三垂线定理可知,B1C⊥BC1,
∴平行四边形BB1C1C为菱形,
此时,BC=BB1,
又∵B1D⊥BC,D为BC中点,B1C=B1B,
∴△BB1C为正三角形,
∴∠B1BC=60°,即α=60°;
(3)过C1作C1E⊥BC于E,则C1E⊥平面ABC,
过E作EF⊥AB于F,连结C1F,
由三垂线定理,得C1F⊥AB,
∴∠C1FE是所求二面角C1-AB-C的平面角,
设AC=BC=AA1=a,在Rt△CC1E中,
由∠C1BE=α=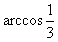 ,C1E=
,C1E=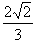 a,
a,
在Rt△BEF中,∠EBF=45°,EF= ,
,
∴∠C1FE=45°,
故所求的二面角C1-AB-C为45°。

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形,∠B1BC=60°,侧面BB1C1C⊥底面ABC,∠ABC=90°,二面角A-B1B-C为30°.
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形,∠B1BC=60°,侧面BB1C1C⊥底面ABC,∠ABC=90°,二面角A-B1B-C为30°. 已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直,BB1=BC,∠B1BC=60°,AB=AC,M是B1C1的中点.
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直,BB1=BC,∠B1BC=60°,AB=AC,M是B1C1的中点. 如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 已知斜三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC,A1B⊥ACl
已知斜三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC,A1B⊥ACl