Question

【题目】如图，椭圆G的中心在坐标原点，其中一个焦点为圆F：x2+y2﹣2x＝0的圆心，右顶点是圆F与x轴的一个交点．已知椭圆G与直线l：x﹣my﹣1＝0相交于A、B两点．

（I）求椭圆的方程；

（Ⅱ）求△AOB面积的最大值．

Answer 1

【答案】（Ⅰ）, （Ⅱ）.

【解析】

（I）设出椭圆方程，圆F的标准方程为（x﹣1）2+y2＝1，圆心为F（1，0），圆与x轴的交点为（0，0）和（2，0），从而可求a＝2，半焦距c＝1，由此能求出椭圆方程；

（Ⅱ）直线与椭圆方程联立．利用韦达定理，求出S△AOB，利用换元法及导数，即可求得S△AOB的最大值．

解：（I）设椭圆方程为（a＞b＞0），圆F的标准方程为（x﹣1）2+y2＝1，

圆心为F（1，0），圆与x轴的交点为（0，0）和（2，0），

由题意a＝2，半焦距c＝1，

∴b2＝a2﹣c2＝4﹣1＝3，

∴椭圆方程为．

（Ⅱ）设A（，）、B（，），

由，消元可得（3m2+3）y2+6my﹣9＝0

∴+，

∴||

∴S△AOB|OF|||

令，则t≥1，m2＝t2﹣1

∴S△AOB

∴S′△AOB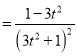

∵t≥1，∴S′△AOB＜0

∴S△AOB在t∈[1，+∞）上是减函数

∴当t＝1时，S△AOB取得最大值，最大值为．