题目内容
已知函数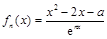 ,其中
,其中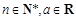 ,
,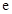 是自然对数的底数.
是自然对数的底数.
(1)求函数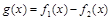 的零点;
的零点;
(2)若对任意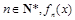 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知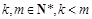 ,且函数
,且函数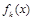 在R上是单调函数,探究函数
在R上是单调函数,探究函数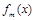 的单调性.
的单调性.
(1)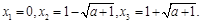 (2)
(2)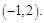 (3)函数
(3)函数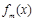 在R上是减函数
在R上是减函数
解析试题分析:(1)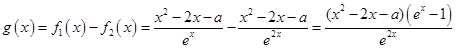
把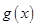 的零点问题转化为方程
的零点问题转化为方程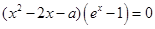 的根的问题.
的根的问题.
(2)因为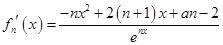 ,由题设可知
,由题设可知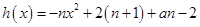 有两个两点,其中一个在
有两个两点,其中一个在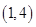 ,一个在
,一个在 外
外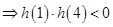 ,解这个不等式,可得实数
,解这个不等式,可得实数 的取值范围.
的取值范围.
(3)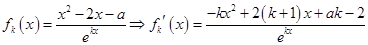
由函数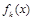 在R上是单调函数,所以
在R上是单调函数,所以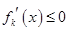 ,得到
,得到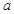 与
与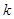 的关系,然后由此关系推出
的关系,然后由此关系推出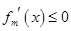 .
.
试题解析:
解:(1)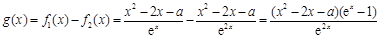 ,
,
令g(x)="0," 有ex-1=0,即x=0;或 x2-2x-a=0;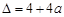 ,
,
①当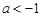 时,
时,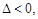 函数
函数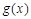 有1个零点
有1个零点 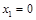 ; 1分
; 1分
②当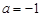 时,
时,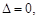 函数
函数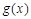 有2个零点
有2个零点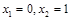 ;2分
;2分
③当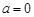 时,
时,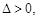 函数
函数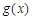 有两个零点
有两个零点 ;3分
;3分
④当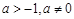 时,
时,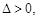 函数
函数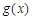 有三个零点:
有三个零点: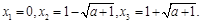 4分
4分
(2)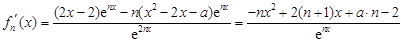 ,5分
,5分
设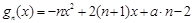 ,
,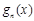 的图像是开口向下的抛物线,
的图像是开口向下的抛物线,
由题意对任意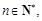
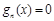 有两个不等实数根
有两个不等实数根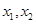 ,
,
且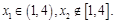 则对任意
则对任意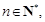
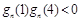 ,
,
即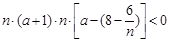 ,有
,有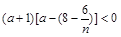 ,7分
,7分
又任意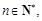
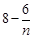 关于
关于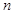 递增,
递增, 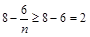 ,
,
故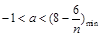 ,所以
,所以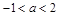 .
.
所以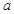 的取值范围是
的取值范围是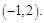 9分
9分
(3)由(2)知, 存在
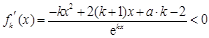 ,又函数
,又函数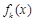 在R上是单调函数,故函数
在R上是单调函数,故函数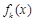 在R上是单调减函数, 10分
在R上是单调减函数, 10分
对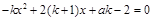 来说
来说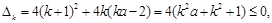 即
即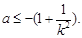 11分
11分
所以对于函数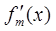 来说
来说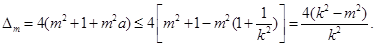
由 知
知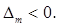 12分
12分
即对任意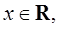
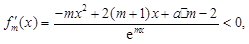
故函数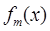 在R上是减函数. 13分
在R上是减函数. 13分
考点:1、函数的零点;2、利用导数研究函数的单调性;3、一元二次方程根的分布.

练习册系列答案
相关题目
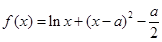 ,
,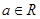 .
. 在
在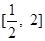 上单调递增,求实数
上单调递增,求实数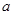 的取值范围;
的取值范围;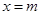 为函数
为函数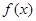 的图象与
的图象与 轴交于
轴交于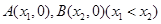 两点,且
两点,且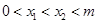 ,
,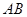 中点为
中点为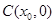 ,
,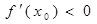 .
.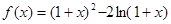
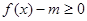 在
在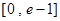 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;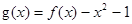 ,若关于x的方程
,若关于x的方程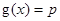 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.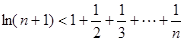
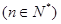
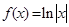
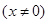 ,函数
,函数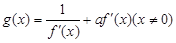
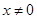 时,求函数
时,求函数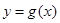 的表达式;
的表达式;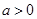 ,函数
,函数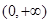 上的最小值是2 ,求
上的最小值是2 ,求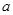 的值.
的值.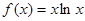 .
. 的单调区间和极值;
的单调区间和极值;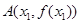 ,
,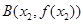 ,且
,且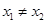 ,证明:
,证明: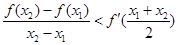 .
. 内的函数
内的函数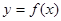 ,若对任意的
,若对任意的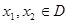 都有
都有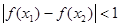 ,则称函数
,则称函数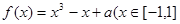 ,(
,(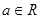 )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.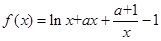 .
.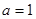 时,求曲线
时,求曲线 在点
在点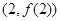 处的切线方程;
处的切线方程;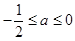 时,讨论
时,讨论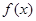 的单调性.
的单调性.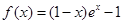 .
.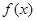 的最大值;
的最大值; ,
, ,且
,且 ,证明:
,证明: .
.
 处,S(t)取得最小值,求此时a的值及S(t)的最小值.
处,S(t)取得最小值,求此时a的值及S(t)的最小值.