题目内容
(1)已知sinα是方程5x2-7x-6=0的根,求sin(-α-
| ||||
cos(
|
(2)已知sinθ+cosθ=0,θ∈R;求sin2θ+2sinθcosθ的值.
分析:(1)根据sinα是方程5x2-7x-6=0的根,得到sinα=-
或sinα=2,舍去不合题意的结果,根据同角的三角函数之间的关系,得到结果.
(2)根据一个角的正弦和余弦之间的关系,得到角的正切值,把所给的三角函数式 加上一个分母1,变成同角的正弦与余弦的平方和,变成正切,得到结果.
| 3 |
| 5 |
(2)根据一个角的正弦和余弦之间的关系,得到角的正切值,把所给的三角函数式 加上一个分母1,变成同角的正弦与余弦的平方和,变成正切,得到结果.
解答:解:(1)∵sinα是方程5x2-7x-6=0的根.
∴sinα=-
或sinα=2(舍).
故sin2α=
,cos2α=
,tan2α=
.
∴原式=
=
=
(2)∵sinθ+cosθ=0,∴tanθ=-1,∴sin2θ+2sinθcosθ=
=
=-
∴sinα=-
| 3 |
| 5 |
故sin2α=
| 9 |
| 25 |
| 16 |
| 25 |
| 9 |
| 16 |
∴原式=
| -cosαcosαtan2α |
| -sinαsinαcos2α |
| 1 |
| cos2α |
| 25 |
| 16 |
(2)∵sinθ+cosθ=0,∴tanθ=-1,∴sin2θ+2sinθcosθ=
| sin2θ+2sinθcosθ |
| sin2θ+cos2θ |
| tan2θ+2tanθ |
| tan2θ+1 |
| 1 |
| 2 |
点评:本题考查同角的三角函数之间的关系,本题解题的关键是熟练应用切与弦之间的互化问题,本题是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
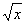 的值等于( )
的值等于( )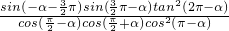 的值.
的值.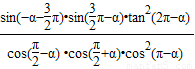 的值.
的值.