题目内容
当0<a<b<1时,下列不等式中正确的是( )
A、(1-a)
| ||
| B、(1+a)a>(1+b)b | ||
C、(1-a)b>(1-a)
| ||
| D、(1-a)a>(1-b)b |
分析:根据指数的单调性,即当底数大于1时单调递增,当底数大于0小于1时单调递减,对选项逐一验证即可得到答案.
解答:解析:∵0<a<1,∴0<1-a<1,
y=(1-a)x为减函数,
又∵0<b<1,∴
>b,b>
,∴(1-a)
<(1-a)b,
(1-a)b<(1-a)
,∴A、C均错,
又∵1<1+a<1+b,∴(1+a)a<(1+b)a<(1+b)b,∴B错.
对于D,(1-a)a>(1-a)b,
而(1-a)b>(1-b)b,∴(1-a)a>(1-b)b.
故选D
y=(1-a)x为减函数,
又∵0<b<1,∴
| 1 |
| b |
| b |
| 2 |
| 1 |
| b |
(1-a)b<(1-a)
| b |
| 2 |
又∵1<1+a<1+b,∴(1+a)a<(1+b)a<(1+b)b,∴B错.
对于D,(1-a)a>(1-a)b,
而(1-a)b>(1-b)b,∴(1-a)a>(1-b)b.
故选D
点评:本题主要考查指数函数的单调性.属基础题.

练习册系列答案
相关题目
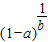 >(1-a)b
>(1-a)b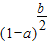
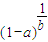 >(1-a)b
>(1-a)b