题目内容
已知函数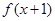 是定义在
是定义在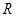 上的奇函数,若对于任意给定的不等实数
上的奇函数,若对于任意给定的不等实数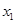 、
、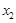 ,不等式
,不等式 恒成立,则不等式
恒成立,则不等式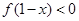 的解集为 .
的解集为 .
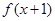 是定义在
是定义在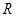 上的奇函数,若对于任意给定的不等实数
上的奇函数,若对于任意给定的不等实数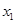 、
、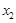 ,不等式
,不等式 恒成立,则不等式
恒成立,则不等式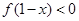 的解集为 .
的解集为 .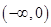
试题分析:先利用不等式(x1-x2)[f(x1)-f(x2)]<0恒成立得到函数f(x)是定义在R上的减函数;再利用函数f(x+1)是定义在R上的奇函数得到函数f(x)过(1,0)点,二者相结合即可求出不等式f(1-x)<0的解集解:由不等式(x1-x2)[f(x1)-f(x2)]<0恒成立得,函数f(x)是定义在R上的减函数 ①.又因为函数f(x+1)是定义在R上的奇函数,所以有函数f(x+1)过点(0,0);故函数f(x)过点(1,0)②.①②相结合得:x>1时,f(x)<0.故不等式f(1-x)<0转化为1-x>1⇒x<0.故答案为
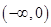
点评:本题主要考查函数奇偶性和单调性的综合应用问题.关键点有两处:①判断出函数f(x)的单调性;②利用奇函数的性质得到函数f(x)过(1,0)点。

练习册系列答案
相关题目
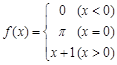 ,则
,则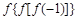 =( )
=( )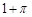
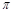
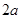 人,(
人,(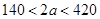 ,且
,且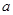 为偶数),每人每年可创利
为偶数),每人每年可创利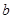 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利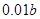 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年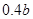 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?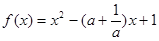 ,
,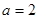 时,解不等式
时,解不等式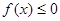 ;
;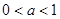 ,解关于
,解关于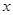 的不等式
的不等式 为全集,
为全集, ,则
,则 ( )
( )



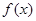 的图象恰好通过
的图象恰好通过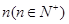 个整点,则称函数
个整点,则称函数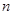 阶整点函数。有下列函数:
阶整点函数。有下列函数: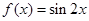 ; ②
; ②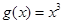 ③
③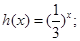 ④
④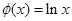 ,
,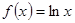 ,
,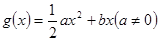
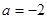 时,
时,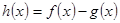 在其定义域内单调递增,求
在其定义域内单调递增,求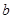 的取值范围;
的取值范围;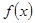 的图象
的图象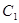 与函数
与函数 的图象
的图象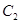 交于
交于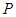 ,
,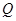 两点,过线段
两点,过线段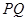 的中点
的中点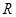 作
作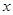 轴的垂线分别交
轴的垂线分别交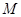 ,
,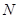 ,问是否存在点
,问是否存在点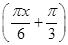 (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.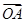 ·
·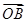 的值;
的值;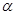 、
、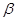 的终边上,求tan(
的终边上,求tan(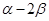 )的值.
)的值.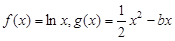 (
(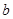 为常数)。
为常数)。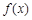 的图象在点(
的图象在点(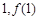 )处的切线与函数
)处的切线与函数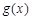 的图象相切,求实数
的图象相切,求实数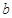 的值;
的值;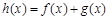 ,若函数
,若函数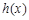 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数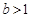 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数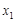 ,
,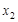 ,都有
,都有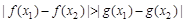 成立,求
成立,求