题目内容
函数f(x)=
．给出函数f（x）下列性质：
（1）f（x）的定义域和值域均为[-1，1]；
（2）f（x）是奇函数
（3）函数在定义域上单调递增；
（4）函数f（x）有两零点；
（5）A、B为函数f（x）图象上任意不同两点，则
＜|AB|≤2．
请写出所有关于函数f（x）性质正确描述的序号．则函数f（x）有关性质中正确描述的个数是（ ）
| ||
| |x-2|-2 |
（1）f（x）的定义域和值域均为[-1，1]；
（2）f（x）是奇函数
（3）函数在定义域上单调递增；
（4）函数f（x）有两零点；
（5）A、B为函数f（x）图象上任意不同两点，则
| 2 |
请写出所有关于函数f（x）性质正确描述的序号．则函数f（x）有关性质中正确描述的个数是（ ）
分析：首先求出函数的定义域，根据x的不同取值范围把函数分段，作出函数图象，根据图象对四个结论逐一进行判断，可以得到正确的结论．
解答：解：由
，得：-1≤x＜0或0＜x≤1．
此时，f(x)=
=-
=
，
函数图象如图所所示，
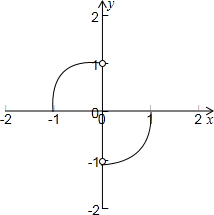
由图象可知（1）错误；（2）正确；（3）错误；（4）正确；（5）错误（0＜|AB|≤2）；
故选B．
|
此时，f(x)=
|x|
| ||
| 2-x-2 |
|x|
| ||
| x |
|
函数图象如图所所示，
由图象可知（1）错误；（2）正确；（3）错误；（4）正确；（5）错误（0＜|AB|≤2）；
故选B．
点评：本题考查的知识点是，判断命题真假，函数的定义域及其求法，函数的值域和函数的零点，考查了数形结合的数学思想，解答此题的关键是正确作出函数图象，此题为中档题．
练习册系列答案
相关题目
已知函数f(x)=
若f（2-a2）＞f（a），则实数a的取值范围是（ ）
|
| A、（-∞，-1）∪（2，+∞） |
| B、（-1，2） |
| C、（-2，1） |
| D、（-∞，-2）∪（1，+∞） |