题目内容
给出下列命题
(1)已知直线m,l,平面α,β,若m⊥β,l?α,α∥β,则m⊥l
(2)
•
>0,是
•
的夹角为锐角的充要条件;
(3)如果函数y=f(x)为奇函数,则f(0)=0
(4)若f'(x0)=0,则f(x0)为极大值或极小值
(5)y=sin(2x+
)的图象的一个对称中心是(
,0)
以上命题正确的是
(1)已知直线m,l,平面α,β,若m⊥β,l?α,α∥β,则m⊥l
(2)
| a |
| b |
| a |
| b |
(3)如果函数y=f(x)为奇函数,则f(0)=0
(4)若f'(x0)=0,则f(x0)为极大值或极小值
(5)y=sin(2x+
| π |
| 3 |
| π |
| 3 |
以上命题正确的是
(1)(5)
(1)(5)
(注:把你认为正确的命题的序号都填上)分析:(1)中,若α∥β,且m⊥α,可得m⊥β,利用线面垂直的性质,可得结论;
(2)
•
>0时,
•
的夹角为锐角或直角;
(3)函数在0处有定义时,结论成立,否则不成立;
(4)根据极值的含义,满足f′(x0)=0,还必须满足在其左右附近导数符号改变;
(5)图象与x轴的交点都是函数的对称中心,故可得结论.
(2)
| a |
| b |
| a |
| b |
(3)函数在0处有定义时,结论成立,否则不成立;
(4)根据极值的含义,满足f′(x0)=0,还必须满足在其左右附近导数符号改变;
(5)图象与x轴的交点都是函数的对称中心,故可得结论.
解答:解:(1)中,若α∥β,且m⊥α⇒m⊥β,又l?β⇒m⊥l,所以(1)正确;
(2)
•
>0时,
•
的夹角为锐角或直角,反之成立,故(2)不正确;
(3)函数在0处有定义时,结论成立,否则不成立,故(3)不正确;
(4)根据极值的含义,满足f′(x0)=0,还必须满足在其左右附近导数符号改变,故(4)不正确;
(5)图象与x轴的交点都是函数的对称中心,当x=
时,y=0,故结论正确
综上知,正确的命题是(1)(5)
故答案为:(1)(5)
(2)
| a |
| b |
| a |
| b |
(3)函数在0处有定义时,结论成立,否则不成立,故(3)不正确;
(4)根据极值的含义,满足f′(x0)=0,还必须满足在其左右附近导数符号改变,故(4)不正确;
(5)图象与x轴的交点都是函数的对称中心,当x=
| π |
| 3 |
综上知,正确的命题是(1)(5)
故答案为:(1)(5)
点评:本题考查线面平行,考查向量的夹角,极值的定义,函数的对称性,综合性强.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 ,平面
,平面 ,若
,若
 ,是
,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件; 为奇函数,则
为奇函数,则
 ,则
,则 为极大值或极小值
为极大值或极小值 的图象的一个对称中心是(
的图象的一个对称中心是( ,0)
,0)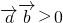 ,是
,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;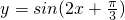 的图象的一个对称中心是
的图象的一个对称中心是
 ,平面
,平面 ,若
,若
 ,是
,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件; 为奇函数,则
为奇函数,则
 ,则
,则 为极大值或极小值
为极大值或极小值 的图象的一个对称中心是(
的图象的一个对称中心是( ,0)
,0)