题目内容
【题目】已知函数![]() 的极大值为
的极大值为![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求实数![]() 的值;
的值;
(2)若函数![]() ,对任意
,对任意![]() ,
,![]() 恒成立.
恒成立.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)证明:![]() .
.
【答案】(1)![]() (2)(i)
(2)(i)![]() (ii)证明见解析
(ii)证明见解析
【解析】
(1)求函数定义域,然后对函数求导,根据函数单调性,得出![]() 时,
时,![]() 有极大值,即可算出实数
有极大值,即可算出实数![]() 的值.
的值.
(2)(i)由(1)知,![]() ,代入
,代入![]() 中,根据
中,根据![]() ,整理至即
,整理至即![]() 对
对![]() 恒成立,设新函数
恒成立,设新函数![]() ,将原问题转化为:
,将原问题转化为:![]() 对
对![]() 恒成立,分
恒成立,分![]() 的取值范围分类讨论即可得出实数
的取值范围分类讨论即可得出实数![]() 的取值范围.(ii)要证
的取值范围.(ii)要证![]() ,
,
转化为证证![]() ,整理至
,整理至![]() ,设两个新函数
,设两个新函数![]() ,
,![]() ,分别对两个新函数求导,判断单调性,即可证得
,分别对两个新函数求导,判断单调性,即可证得![]() 成立.
成立.
解:(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
所以当![]() ,
,![]() 为增函数,当
为增函数,当![]() ,
,![]() 为减函数,
为减函数,
所以![]() 时,
时,![]() 有极大值
有极大值![]() ,
,
所以![]() ;
;
(2)(i)由(1)知,![]() ,
,
则![]() ,即
,即![]() 对
对![]() 恒成立,
恒成立,
所以![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
设![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
![]() ,
,
设![]() ,
,![]() ,
,
原问题转化为:![]() 对
对![]() 恒成立,
恒成立,
①若![]() ,当
,当![]() 时,
时,
![]()
则![]() ,
,
不合题意;
②若![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
符合题意
③若![]() ,则
,则![]() ,
,
令![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 为减函数,
为减函数,
当![]() 时,
时,![]() 为增函数,
为增函数,
所以![]() ,
,
即![]() ,即
,即![]() ;
;
综上![]() .
.
(ii)要证![]() ,
,
只需证![]() ,
,
即![]() ,即
,即![]() ,
,
只需证![]() ,
,
设![]() ,
,![]() ,
,
因为![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() :
:
因为![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,则
,则![]() ,则
,则![]() ,
,
由(2)可知,![]() ,所以
,所以![]() ;
;
所以![]() ,
,
即![]() ,得证.
,得证.
所以 ![]() 成立.
成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在“互联网+”时代的今天,移动互联快速发展,智能手机(Smartphone)技术不断成熟,尤其在5G领域,华为更以![]() 件专利数排名世界第一,打破了以往由美、英、日垄断的前三位置,再次荣耀世界,而华为的价格却不断下降,远低于苹果;智能手机成为了生活中必不可少的工具,学生是对新事物和新潮流反应最快的一个群体之一,越来越多的学生在学校里使用手机,为了解手机在学生中的使用情况,对某学校高二年级
件专利数排名世界第一,打破了以往由美、英、日垄断的前三位置,再次荣耀世界,而华为的价格却不断下降,远低于苹果;智能手机成为了生活中必不可少的工具,学生是对新事物和新潮流反应最快的一个群体之一,越来越多的学生在学校里使用手机,为了解手机在学生中的使用情况,对某学校高二年级![]() 名同学使用手机的情况进行调查,针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如下的数据:
名同学使用手机的情况进行调查,针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如下的数据:
使用时间(小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
所占比例 | 4% | 10% | 31% | 16% |
| 12% | 2% |
(1)求表中![]() 的值;
的值;
(2)从该学校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于![]() 小时的概率?若能,请算出这个概率;若不能,请说明理由;
小时的概率?若能,请算出这个概率;若不能,请说明理由;
(3)若从使用手机![]() 小时和
小时和![]() 小时的两组中任取两人,调查问卷,看看他们对使用手机进行娱乐活动的看法,求这
小时的两组中任取两人,调查问卷,看看他们对使用手机进行娱乐活动的看法,求这![]() 人都使用
人都使用![]() 小时的概率.
小时的概率.
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.

(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为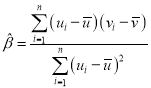 ,
,![]()
【题目】2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
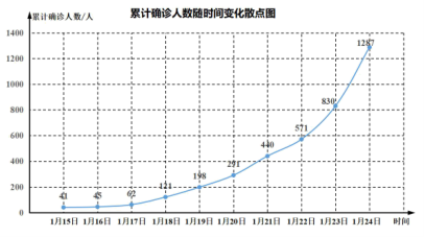
为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数y与时间变量t的两个回归模型,根据1月15日至1月24日的数据(时间变量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
(2根据(1)的判断结果及附表中数据,建立y关于x的回归方程;
(3)以下是1月25日至1月29日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1则认为模型可靠,请判断(2)的回归方程是否可靠?
(ⅱ)2020年1月24日在人民政府的强力领导下,全国人民共同采取了强力的预防“新冠肺炎”的措施,若采取措施5天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?
附:对于一组数据(![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为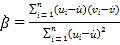 ,
,![]() .
.
参考数据:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |