题目内容
系数矩阵为 ,解为
,解为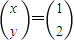 的一个线性方程组是 .
的一个线性方程组是 .
【答案】分析:先根据系数矩阵,写出线性方程组,再利用方程组的解,求出待定系数,从而可得线性方程组.
解答:解:可设线性方程组为
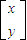 =
= ,
,
由于方程组的解是 ,
,
∴ =
= ,
,
∴所求方程组为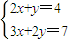 ,
,
故答案为: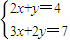 .
.
点评:本题的考点是二元一次方程组的矩阵形式,主要考查待定系数法求线性方程组,应注意理解方程组解的含义.
解答:解:可设线性方程组为

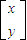 =
= ,
,由于方程组的解是
 ,
,∴
 =
= ,
,∴所求方程组为
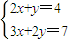 ,
,故答案为:
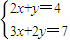 .
.点评:本题的考点是二元一次方程组的矩阵形式,主要考查待定系数法求线性方程组,应注意理解方程组解的含义.

练习册系列答案
相关题目
 ,解为
,解为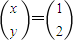 的一个线性方程组是 .
的一个线性方程组是 .