题目内容
将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形与圆的面积之和最小,正方形的周长应为 .
【答案】分析:正确理解题意,充分应用正方形的知识和圆的知识,表示出两种图形的面积.构造目标函数后结合目标函数的特点--一元二次函数,利用二次函数的性质求最值.
解答:解析:设正方形周长为x,则圆的周长为1-x,半径r=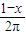 .
.
∴S正=(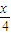 )2=
)2=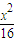 ,S圆=π•
,S圆=π•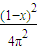 .
.
∴S正+S圆=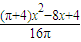 (0<x<1).
(0<x<1).
∴当x=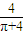 时有最小值.
时有最小值.
答案:
点评:本题充分考查了正方形和圆的知识,目标函数的思想还有一元二次函数求最值的知识.在解答过程当中要时刻注意定义域优先的原则.
解答:解析:设正方形周长为x,则圆的周长为1-x,半径r=
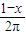 .
.∴S正=(
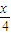 )2=
)2=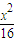 ,S圆=π•
,S圆=π•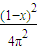 .
.∴S正+S圆=
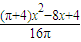 (0<x<1).
(0<x<1).∴当x=
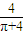 时有最小值.
时有最小值.答案:

点评:本题充分考查了正方形和圆的知识,目标函数的思想还有一元二次函数求最值的知识.在解答过程当中要时刻注意定义域优先的原则.

练习册系列答案
相关题目