题目内容
已知焦点在 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为 ,且过点
,且过点 (题干自编)
(题干自编)
(I)求椭圆C的方程;
(II)直线 分别切椭圆C与圆
分别切椭圆C与圆
 (其中
(其中 )于
)于 两点,求
两点,求 的最大值。
的最大值。
【答案】
解(I)设椭圆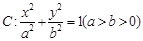 ,则
,则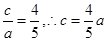 ,
,
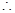
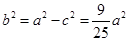 ………………2分
………………2分
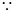 椭圆过点
椭圆过点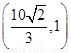 ,
,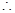
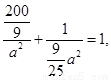 解得
解得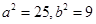 ………………3分
………………3分
椭圆方程为 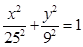 ………………4分
………………4分
(II)设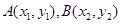 分别为直线
分别为直线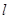 与椭圆和圆的切点,直线
与椭圆和圆的切点,直线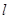 的方程为:
的方程为: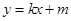 。
。
由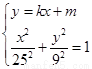 消去
消去 得:
得: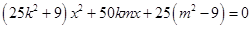
由于直线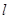 与椭圆相切,所以
与椭圆相切,所以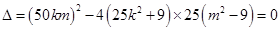
从而可得: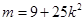 ①
①
 ②………………7分
②………………7分
由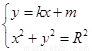 消去
消去 得:
得: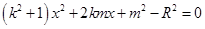
由于直线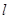 与圆相切,所以
与圆相切,所以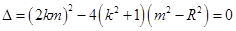
从而可得: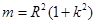 ③
③
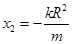 ④………………9分
④………………9分
由 ②④得:
由①③得:  ………………10分
………………10分
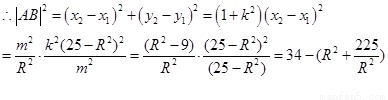 ………………11分
………………11分
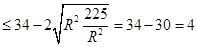 ………………11分
………………11分
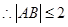

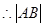 最大值为2. ………………13分
最大值为2. ………………13分
【解析】略

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 轴上、中心在原点的椭圆上一点到两焦点的距离之和为
轴上、中心在原点的椭圆上一点到两焦点的距离之和为 ,若该椭圆的离心率
,若该椭圆的离心率 ,则椭圆的方程是 ( )
,则椭圆的方程是 ( ) B.
B. C.
C.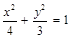 D.
D.
 轴上、中心在原点的椭圆上一点到两焦点的距离之和为
轴上、中心在原点的椭圆上一点到两焦点的距离之和为 ,若该椭圆的离心率
,若该椭圆的离心率 ,则椭圆的方程是( )
,则椭圆的方程是( ) B.
B. C.
C. D.
D.
 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为 ,且过点
,且过点
 分别切椭圆C与圆
分别切椭圆C与圆 (其中
(其中 )于A.B两点,求|AB|的最大值。
)于A.B两点,求|AB|的最大值。 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为 ,且过点
,且过点
 分别切椭圆C与圆
分别切椭圆C与圆 (其中
(其中 )于A、B两点,求|AB|的最大值。
)于A、B两点,求|AB|的最大值。