题目内容
已知焦点在 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为 ,且过点
,且过点
(1)求椭圆C的方程;
(2)直线 分别切椭圆C与圆
分别切椭圆C与圆 (其中
(其中 )于A、B两点,求|AB|的最大值。
)于A、B两点,求|AB|的最大值。
【答案】
解:(1)设椭圆的方程为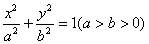 ,则
,则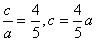 ,
,

 椭圆过点
椭圆过点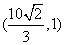
 ,
,
解处 故椭圆C的方程为
故椭圆C的方程为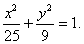 6分
6分
(2)设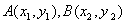 分别为直线
分别为直线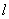 与椭圆和圆的切点,
与椭圆和圆的切点,
直线AB的方程为: 因为A既在椭圆上,又在直线AB上,
因为A既在椭圆上,又在直线AB上,
从而有 ,
,
消去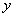 得:
得: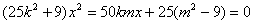
由于直线与椭圆相切, 故
从而可得: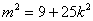 ①
① 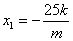 ②……8分
②……8分
由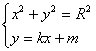 消去
消去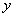 得:
得: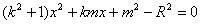
由于直线与圆相切,得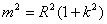 ③
③ 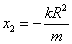 ④
④
由②④得: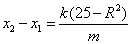 由①③得:
由①③得: ……10分
……10分
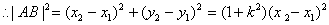
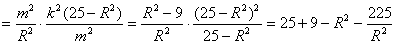
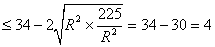
即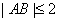 ,当且仅当
,当且仅当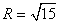 时取等号,所以|AB|的最大值为2。……12分
时取等号,所以|AB|的最大值为2。……12分

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为 ,且过点
,且过点 (题干自编)
(题干自编) 分别切椭圆C与圆
分别切椭圆C与圆
 (其中
(其中 )于
)于 两点,求
两点,求 的最大值。
的最大值。 轴上、中心在原点的椭圆上一点到两焦点的距离之和为
轴上、中心在原点的椭圆上一点到两焦点的距离之和为 ,若该椭圆的离心率
,若该椭圆的离心率 ,则椭圆的方程是 ( )
,则椭圆的方程是 ( ) B.
B. C.
C.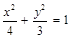 D.
D.
 轴上、中心在原点的椭圆上一点到两焦点的距离之和为
轴上、中心在原点的椭圆上一点到两焦点的距离之和为 ,若该椭圆的离心率
,若该椭圆的离心率 ,则椭圆的方程是( )
,则椭圆的方程是( ) B.
B. C.
C. D.
D.
 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为 ,且过点
,且过点
 分别切椭圆C与圆
分别切椭圆C与圆 (其中
(其中 )于A.B两点,求|AB|的最大值。
)于A.B两点,求|AB|的最大值。