题目内容
已知f(x)=log2(x﹣1),若实数m,n满足f(m)+f(n)=2,则mn的最小值是 .
9
试题分析:由题目给出的函数解析式可以得到m和n均大于1,然后由f(m)+f(n)=2,得到mn﹣(m+n)=3.利用基本不等式转化为含mn的不等式,通过解不等式可以求得mn的最小值.
由f(x)=log2(x﹣1),且实数m,n满足f(m)+f(n)=2,
所以log2(m﹣1)+log2(n﹣1)=2.
则
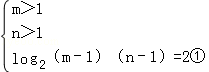 ,
,由①得(m﹣1)(n﹣1)=4,即mn﹣(m+n)=3.
所以3=mn﹣(m+n)
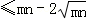 .
.即
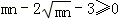 .解得
.解得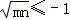 ,或
,或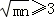 .
.因为m>1,n>1.所以
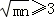 ,mn≥9.
,mn≥9.点评:本题考查了基本不等式,考查了利用基本不等式求最值,考查了对数函数的性质,利用了数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
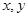 满足
满足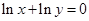 ,且
,且 恒成立,则
恒成立,则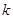 的取值范围是________.
的取值范围是________. =log36,b=log510,c=log714,则
=log36,b=log510,c=log714,则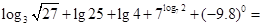
 ,则函数
,则函数 的定义域是 .
的定义域是 .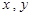 ,都有
,都有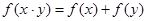 ”的函数可以是( )
”的函数可以是( )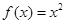
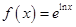
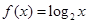
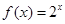
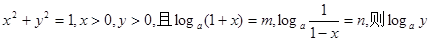 等于( )
等于( )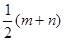
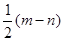
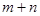
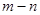
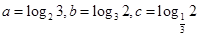 ,则
,则 的大小关系是( )
的大小关系是( )


