题目内容
【题目】在盒子里有大小相同，仅颜色不同的乒乓球共10个，其中红球4个，白球3个，蓝球3个。
(Ⅰ)现从中任取出一球确定颜色后放回盒子里，再取下一个球，重复以上操作，最多取3次，过程中如果取出蓝色球则不再取球，求：
①最多取两次就结束的概率；
②整个过程中恰好取到2个白球的概率；
(Ⅱ)若改为从中任取出一球确定颜色后不放回盒子里，再取下一个球。重复以上操作，最多取3次，过程中如果取出蓝色球则不再取球，则设取球的次数为随机变量
求
的分布列和数学期望,
【答案】(Ⅰ)①
，②
；(Ⅱ)答案见解析.
【解析】
(Ⅰ)①由题意分别求得取1次结束和取2次结束的概率即可确定满足题意的概率；
②首先列出所有取到2个白球的事件，然后利用概率公式可得相应的概率值；
(Ⅱ)由题意可知
的取值为 1,2,3 ，求得相应的概率值即可确定分布列，进一步计算数学期望即可.
(Ⅰ)①设取球的次数为
，
则
，
，
故最多取两次就结束的概率
.
②由题意可知，可以如下取球：红白白，白红白，白白红，白白蓝，
所以恰好取到 2 个白球的概率：
.
(Ⅱ)随机变量的取值为 1,2,3 ，
，
，
随机变量的分布列为：
| 1 | 2 | 3 |
|
|
|
|
的数学期望
.
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
【题目】
大学就业指导中心对该校毕业生就业情况进行跟踪调查，发现不同的学历对就业专业是否为毕业所学专业有影响，就业指导中心从
届的毕业生中，抽取了本科和研究生毕业生各
名，得到下表中的数据.
就业专业 毕业学历 | 就业为所学专业 | 就业非所学专业 |
本科 |
|
|
研究生 |
|
|
（1）根据表中的数据，能否在犯错概率不超过
的前提下认为就业专业是否为毕业所学专业与毕业生学历有关；
（2）为了进一步分析和了解本科毕业生就业的问题，按分层抽样的原则从本科毕业生中抽取一个容量为
的样本，要从人中任取
人参加座谈，求被选取的人中至少有
人就业非毕业所学专业的概率.
附：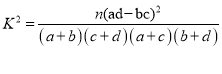
,
|
|
|
|
|
|
|
|
|
|
|
|
【题目】研学旅行是研究性学习和旅行体验相结合的校外教育活动，继承和发展了我国传统游学、“读万卷书，行万里路”的教育理念和人文精神，成为素质教育的新内容和新方式，提升中小学生的自理能力、创新精神和实战能力，是综合实战育人的有效途径，为了了解某校高二年级600名学生在一次研学旅行活动中的武术表演情况，研究人员在该校高二学生中随机抽取了10名学生的武术表演成绩进行统计，统计结果如图所示（满分100分），已知这10名学生或武术表演的平均成绩为85分.
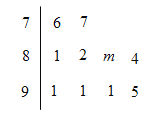
（1）求m的值；
（2）为了研究高二男、女生的武术表演情况，现对该校高二所有学生的武术表演成绩进行分类统计，得到的数据如下表所示：
男生 | 女生 | 合计 | |
武术表演成绩超过80分 | 150 | ||
武术表演成绩不超过80分 | 100 | ||
合计 |
已知随机抽取这600名学生中的一名学生，抽到武术表演成绩超过80分的学生概率是
，根据已知条件完成上面
列联表，并据此判断是否有
的把握认为武术表演成绩超过80分与性别具有相关性.
参考公式：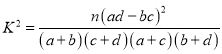
，其中
.
临界值表：
P（ | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
