Question

已知函数f（x）=x²-2lnx+a（a为实常数）．
（1）求f（x）的单调区间；
（2）求f（x）在区间[

1

2

，2]上的最大值与最小值．

Answer 1

（1）函数f（x）的定义域为{x|x＞0}，f′（x）=2x-

2

x

，
令f′（x）＞0，有

x2-1＞0 x＞0

，解之得x＞1，
令f′（x）＜0，有

x2-1＜0 x＞0

，得0＜x＜1，
所以函数f（x）的单调减区间为（0，1），f（x）的单调增区间为（1，+∞）．
（2）当x在[

1

2

，2]上变化时，f'（x），f（x）的变化情况如下表：

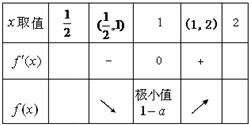
由表知，函数f（x）_min=1-a，
又f(

1

2

)=(

1

2

)2-2ln

1

2

+a=

1

4

+2ln2+a，f（2）=2²-2ln2+a=4-2ln2+a，
f(

1

2

)-f(2)=(

1

4

+2ln2+a)-(4-2ln2+a)=4ln2-

15

4

＜0，
所以f（x）_max=4-2ln2+a．