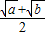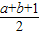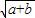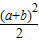题目内容
若a、b、x、y均为正实数,并且x+y=1,求证:ab≤(ax+by)(ay+bx)≤
.
| (a+b)2 | 4 |
分析:依题意,先作差(ax+by)(ay+bx)-ab后化积即可证得ab≤(ax+by)(ay+bx),再利用基本不等式对(ax+by)(ay+bx)放缩,即可证得(ax+by)(ay+bx)≤
,从而原结论可证.
| (a+b)2 |
| 4 |
解答:证明:∵(ax+by)(ay+bx)-ab=a2xy+b2xy+abx2+aby2-ab
=xy(a2+b2)+ab(x2+y2-1)
=xy(a2+b2)+ab[(x+y)2-2xy-1].
∵a、b、x、y均为正实数,x+y=1,
∴(ax+by)(ay+bx)-ab
=xy(a2+b2)-2abxy
=xy(a-b)2≥0,
∴ab≤(ax+by)(ay+bx).
又(ax+by)(ay+bx)≤[
]2=[
]2=(
)2=
.
∴ab≤(ax+by)(ay+bx)≤
.
=xy(a2+b2)+ab(x2+y2-1)
=xy(a2+b2)+ab[(x+y)2-2xy-1].
∵a、b、x、y均为正实数,x+y=1,
∴(ax+by)(ay+bx)-ab
=xy(a2+b2)-2abxy
=xy(a-b)2≥0,
∴ab≤(ax+by)(ay+bx).
又(ax+by)(ay+bx)≤[
| (ax+by)+(ay+bx) |
| 2 |
| a(x+y)+b(x+y) |
| 2 |
| a+b |
| 2 |
| (a+b)2 |
| 4 |
∴ab≤(ax+by)(ay+bx)≤
| (a+b)2 |
| 4 |
点评:本题考查不等式的证明,着重考查作差法与放缩法的综合应用,考查推理证明的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a,b,x,y均为正数,且a,b为常数,x,y为变量,若x+y=1,则
+
的最大值为( )
| ax |
| by |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
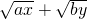 的最大值为
的最大值为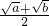

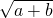
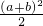
 的最大值为( )
的最大值为( )