题目内容
在∆ABC中,tanA是以-4为第三项,4为第七项的等差数列的公差,tanB是以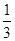 为第三项,9为第六项的等比数列的公比,则这个三角形是
为第三项,9为第六项的等比数列的公比,则这个三角形是
| A.钝角三角形 | B.锐角三角形 | C.等腰直角三角形 | D.以上都不对 |
B
解析试题分析:以数列为背景,建立得到角的关系式,进而结合两角和差的三角函数关系式,得到A+B的值, 进而得到三角形的形状。
因为tanA是以-4为第三项,4为第七项的等差数列的公差,则等差数列的通项公式可知,4-(-4)=4tanA,tanA=2,
根据tanB是以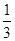 为第三项,9为第六项的等比数列的公比,则由等比数列的通项公式可知
为第三项,9为第六项的等比数列的公比,则由等比数列的通项公式可知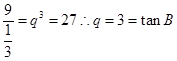 ,而tan(A+B)=
,而tan(A+B)= 
根据A,C,B的正切值为正数,说明了都是锐角,因此可知选B.
考点:本试题主要是考查了等差数列和等比数列的通项公式。
点评:确定三角形的形状问题,一般先由已知得到角的关系式,或者是边的关系时候,然后化简分析得到结论,同时要结合三角函数的公式来化简,体现了三角与数列的知识交汇运用。

练习册系列答案
相关题目
已知等比数列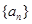 的公比为正数,且
的公比为正数,且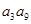 =
=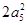 ,
,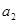 =1,则
=1,则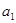 = ( )
= ( )
A.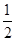 | B.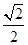 | C.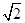 | D.2 |
 的内角
的内角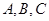 的对边分别为
的对边分别为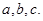 若
若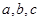 成等比数列,且
成等比数列,且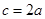 ,则
,则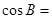 ( )
( )
A.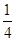 | B.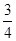 | C. | D.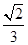 |
设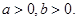 若
若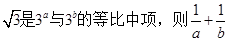 的最小值( )
的最小值( )
A.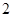 | B. | C.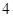 | D.8 |
等比数列{ }中,
}中, ,前3项之和
,前3项之和 ,则数列{
,则数列{ }的公比为( )
}的公比为( )
| A.1 | B.1或 | C. | D.-1或 |
等比数列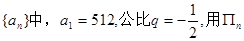 表示它的前n项之积,即
表示它的前n项之积,即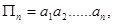 则
则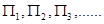 中最大的是( )
中最大的是( )
A.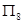 | B. | C.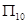 | D.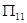 |
在等比数列 中,已知
中,已知 ,
, ,则
,则
| A.9 | B.65 | C.72 | D.99 |
已知等比数列 满足
满足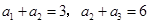 ,则
,则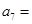 ( )
( )
| A.64 | B.81 | C.128 | D.243 |
设 为等比数列
为等比数列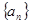 的前
的前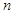 项和,若
项和,若 ,则
,则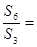 ( )
( )
| A.8 | B.9 | C.15 | D.16 |