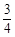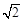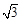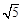题目内容
等比数列{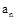 }中,
}中, ,前3项之和
,前3项之和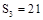 ,则数列{
,则数列{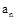 }的公比为( )
}的公比为( )
| A.1 | B.1或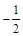 | C.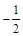 | D.-1或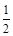 |
B
解析试题分析:设公比为 ,因为
,因为 ,所以
,所以 ………………①
………………①
因为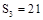 ,所以
,所以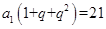 ………………………………②
………………………………②
①÷②,得: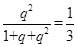 ,解得
,解得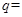 1或
1或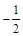 。
。
考点:等比数列的性质。
点评:解数列的有关问题,最基本的方法是:根据题意列出方程,组成方程组求解。而对等比数列来说,解方程组常用的方法是两式相除消元。

练习册系列答案
相关题目
已知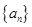 是等比数列,
是等比数列,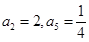 ,则公比
,则公比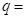 ( )
( )
A.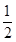 | B.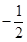 | C. | D.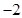 |
设等比数列{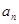 }的前
}的前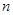 项和为
项和为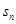 若
若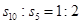 ,则
,则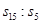 = ( )
= ( )
| A.3:4 | B.2:3 | C.1:2 | D.1:3 |
等比数列 的各项均为正数,且
的各项均为正数,且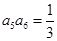 ,则
,则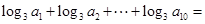 ( )
( )
A.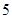 | B.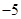 | C. | D.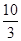 |
在∆ABC中,tanA是以-4为第三项,4为第七项的等差数列的公差,tanB是以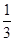 为第三项,9为第六项的等比数列的公比,则这个三角形是
为第三项,9为第六项的等比数列的公比,则这个三角形是
| A.钝角三角形 | B.锐角三角形 | C.等腰直角三角形 | D.以上都不对 |
等比数列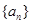 的前
的前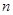 项和为
项和为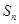 ,若
,若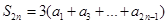 ,
,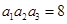 ,则
,则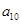 等于( )
等于( )
| A.-512 | B.1024 | C.-1024 | D.512 |
在等比数列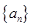 中,
中,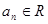 (
( ),
),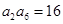 ,
,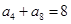 ,则
,则 =( )
=( )
A.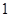 | B. | C.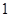 或 或 | D.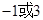 |
已知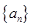 是等比数列,
是等比数列, ,
,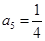 ,则
,则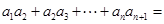 ( )
( )
A.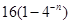 | B.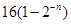 |
C. | D.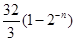 |
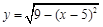 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )