题目内容
(本小题满分12分)已知双曲线![]() (a>0,b>0)的上、下顶点分别为A、B,一
(a>0,b>0)的上、下顶点分别为A、B,一
个焦点为F(0,c)(c>0),两准线间的距离为1,|AF|、|AB|、|BF|成等差数列.
(1)求双曲线的方程;
(2)设过点F作直线l交双曲线上支于M、N两点,如果S△MON=![]() tan∠MON,求△MBN的面积.
tan∠MON,求△MBN的面积.
解:(I)由已知|AF|=c-a,AB=2a,|BF|= c+a,
∴ 4a=(c-a)+(c+a),即c=2a.
∵ ![]() ,于是可解得a=1,c=2,b2=c2-a2=3.∴ 双曲线方程为
,于是可解得a=1,c=2,b2=c2-a2=3.∴ 双曲线方程为![]() . ……………4分
. ……………4分
(II)∵ S△MON= ![]() ,
,
∴ ![]()
整理得|OM|·|ON|·cos![]() MON=-7,即
MON=-7,即![]() . ……………………6分
. ……………………6分
设M(x1,y1),N(x2,y2),于是![]() ,
,![]() ,
,
∴ x1x2+y1y2=-7.
设直线MN的斜率为k,则MN的方程为y=kx+2.
∴ 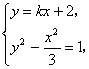 消去y,整理得(3k2-1)x2+12kx+9=0. ………………………8分
消去y,整理得(3k2-1)x2+12kx+9=0. ………………………8分
∵ MN与双曲线交于上支,
∴ Δ=(12k)2-4×9×(![]() )=36k2+36>0, x1x2
)=36k2+36>0, x1x2![]() ,
,![]() ,
,
∴ ![]() . ………………………9分
. ………………………9分
∴ x1x2+(kx1+2)(kx2+2)=-7,整理得x1x2+k2x1x2+2k(x1+x2)+4=-7,
代入得:![]() ,
,
解得![]() ,满足条件. ……10分
,满足条件. ……10分
S△MBN=![]() =
=![]()
![]()
=![]()
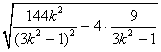
=![]() =
=![]() . ……………………………………………12分
. ……………………………………………12分

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目