题目内容
 (2013•惠州二模)正方体ABCD_A1B1C1D1,AA1=2,E为棱CC1的中点.
(2013•惠州二模)正方体ABCD_A1B1C1D1,AA1=2,E为棱CC1的中点.(Ⅰ)求证:B1D1⊥AE;
(Ⅱ)求证:AC∥平面B1DE;
(Ⅲ)求三棱锥A-BDE的体积.
分析:(I)先证BD⊥面ACE,再利用线面垂直的性质,即可证得结论;
(II)连接AF、CF、EF,由E、F是CC1、BB1的中点,易得AF∥ED,CF∥B1E,从而可证平面ACF∥面B1DE.进而由面面平行的性质可得AC∥平面B1DE;
(Ⅲ)三棱锥A-BDE的体积,即为三棱锥E-ABD的体积,根据正方体棱长为2,E为棱CC1的中点,代入棱锥体积公式,可得答案.
(II)连接AF、CF、EF,由E、F是CC1、BB1的中点,易得AF∥ED,CF∥B1E,从而可证平面ACF∥面B1DE.进而由面面平行的性质可得AC∥平面B1DE;
(Ⅲ)三棱锥A-BDE的体积,即为三棱锥E-ABD的体积,根据正方体棱长为2,E为棱CC1的中点,代入棱锥体积公式,可得答案.
解答: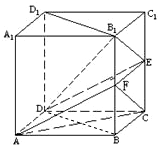 证明:(1)连接BD,则BD∥B1D1,(1分)
证明:(1)连接BD,则BD∥B1D1,(1分)
∵ABCD是正方形,∴AC⊥BD.
∵CE⊥面ABCD,∴CE⊥BD.
又AC∩CE=C,∴BD⊥面ACE.(4分)
∵AE?面ACE,∴BD⊥AE,
∴B1D1⊥AE.(5分)
(2)连接AF、CF、EF.
∵E、F是CC1、BB1的中点,∴CE平行且等于B1F,
∴四边形B1FCE是平行四边形,
∴CF∥B1E,CF?平面B1DE,B1E?平面B1DE(7分)
∴CF∥平面B1DE
∵E,F是CC1、BB1的中点,∴EF平行且等于BC
又BC平行且等于AD,∴EF平行且等于AD.
∴四边形ADEF是平行四边形,∴AF∥ED,
∵AF?平面B1DE,ED?平面B1DE(7分)
∴AF∥平面B1DE
∵AF∩CF=F,
∴平面ACF∥平面B1DE.(9分)
又∵AC?平面ACF
∴AC∥平面B1DE;
解:(Ⅲ)三棱锥A-BDE的体积,即为三棱锥E-ABD的体积
∴V=
•
•AD•AB•EC=
•
•2•2•1=
 证明:(1)连接BD,则BD∥B1D1,(1分)
证明:(1)连接BD,则BD∥B1D1,(1分)∵ABCD是正方形,∴AC⊥BD.
∵CE⊥面ABCD,∴CE⊥BD.
又AC∩CE=C,∴BD⊥面ACE.(4分)
∵AE?面ACE,∴BD⊥AE,
∴B1D1⊥AE.(5分)
(2)连接AF、CF、EF.
∵E、F是CC1、BB1的中点,∴CE平行且等于B1F,
∴四边形B1FCE是平行四边形,
∴CF∥B1E,CF?平面B1DE,B1E?平面B1DE(7分)
∴CF∥平面B1DE
∵E,F是CC1、BB1的中点,∴EF平行且等于BC
又BC平行且等于AD,∴EF平行且等于AD.
∴四边形ADEF是平行四边形,∴AF∥ED,
∵AF?平面B1DE,ED?平面B1DE(7分)
∴AF∥平面B1DE
∵AF∩CF=F,
∴平面ACF∥平面B1DE.(9分)
又∵AC?平面ACF
∴AC∥平面B1DE;
解:(Ⅲ)三棱锥A-BDE的体积,即为三棱锥E-ABD的体积
∴V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题主要考查线面垂直和面面平行,解题的关键是正确运用线面垂直和面面平行的判定定理,属于中档题.

练习册系列答案
相关题目