题目内容
16.用秦九韶算法求多项式f(x)=208+9x2+6x4+x6,在x=-4时,v2的值为( )| A. | -4 | B. | 1 | C. | 17 | D. | 22 |
分析 先将多项式改写成如下形式:f(x)=(((((x)x+6)x)x+9)x)x+208,将x=-4代入并依次计算v0,v1,v2的值,即可得到答案.
解答 解:∵f(x)=208+9x2+6x4+x6=(((((x)x+6)x)x+9)x)x+208,
当x=-4时,
v0=1,
v1=1×(-4)=-4,
v2=-4×(-4)+6=22,
故选:D
点评 本题考查的知识点是秦九韶算法,其中熟练掌握秦九韶算法的运算法则,是解答本题的关键.

练习册系列答案
相关题目
5.已知函数f(x)=x(1+a|x|)(a∈R),设关于x的不等式f(x+a)<f(x)的解集为A,若$[{-\frac{1}{2},\frac{1}{2}}]⊆A$,则实数a的取值范围是( )
| A. | (-1,0) | B. | $({-1,\frac{{1-\sqrt{5}}}{2}})$ | C. | $({\frac{{1-\sqrt{5}}}{2},0})$ | D. | $({0,\frac{{1+\sqrt{5}}}{2}})$ |
6.不等$\frac{1}{a-b}+\frac{1}{b-c}+\frac{λ}{c-a}<0$对满足a>b>c恒成立,则λ的取值范围 ( )
| A. | (-∞,0] | B. | (-∞,1) | C. | (-∞,4] | D. | (4,+∞) |
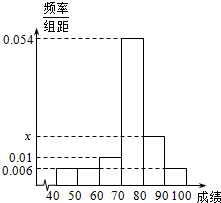 某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].