题目内容
若
，则
（ ）
A. 
B. 
C. 
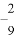D. 
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
教学练新同步练习系列答案课前课后同步练习系列答案课堂小作业系列答案黄冈小状元口算速算练习册系列答案成功训练计划系列答案倍速训练法直通中考考点系列答案题目内容
若，则（ ）
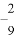A. B. C. D.
教学练新同步练习系列答案课前课后同步练习系列答案课堂小作业系列答案黄冈小状元口算速算练习册系列答案成功训练计划系列答案倍速训练法直通中考考点系列答案
，
满足
则目标函数
的最大值为（ ）
B. 
C. 
D. 
（
）与圆
交于不同的两点
、
，
是坐标原点，且有
，那么
的取值范围是（ ）
B．
C．
D．
）
（其中
）的图象不可能是（ ）
B. 
C. 
D. 
过两点
,且圆心
上.
是直线
上的动点，
是圆
为切点，求四边形
面积的最小值.
与平面
垂直，则直线
经过点
，且离心率
.
的方程；
能否作出直线
，使
两点，且以
为直径的圆经过坐标原点
？若存在,求出直线
除以
的余数），若输入的m，n分别为485，135，则输出的m=（ ）