题目内容
在△ABC中,给出下列四个结论:
(1)若sin2A=sin2B,则△ABC是等腰三角形;
(2)若sinA=sinB,则△ABC是等腰三角形;
(3)若
=
=c,则△ABC是直角三角形;
(4)若sinA>sinB,则A>B.
其中正确命题的序号是______.
(1)若sin2A=sin2B,则△ABC是等腰三角形;
(2)若sinA=sinB,则△ABC是等腰三角形;
(3)若
| a |
| sinA |
| b |
| sinB |
(4)若sinA>sinB,则A>B.
其中正确命题的序号是______.
(1)△ABC中,∵sin2A=sin2B,
∴2A=2B或2A=π-2B,即A=B或A+B=
,
∴△ABC是等腰三角形或是直角三角形,故(1)错误;
(2)△ABC中,∵sinA=sinB,
由正弦定理知,sinA=
,sinB=
,
∴a=b,
∴△ABC是等腰三角形,故(2)正确;
(3)∵
=
=
=c,
∴sinC=1,
∴C=
,
∴△ABC是直角三角形,故(3)正确;
(4)由正弦定理知sinA=
,sinB=
,
∴sinA>sinB?
>
?a>b,
在△ABC中,“大边”对“大角”,
∴A>B,故(4)正确;
综上所述,正确命题的序号是(2)(3)(4).
故答案为:(2)(3)(4).
∴2A=2B或2A=π-2B,即A=B或A+B=
| π |
| 2 |
∴△ABC是等腰三角形或是直角三角形,故(1)错误;
(2)△ABC中,∵sinA=sinB,
由正弦定理知,sinA=
| a |
| 2R |
| b |
| 2R |
∴a=b,
∴△ABC是等腰三角形,故(2)正确;
(3)∵
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴sinC=1,
∴C=
| π |
| 2 |
∴△ABC是直角三角形,故(3)正确;
(4)由正弦定理知sinA=
| a |
| 2R |
| b |
| 2R |
∴sinA>sinB?
| a |
| 2R |
| b |
| 2R |
在△ABC中,“大边”对“大角”,
∴A>B,故(4)正确;
综上所述,正确命题的序号是(2)(3)(4).
故答案为:(2)(3)(4).

练习册系列答案
相关题目
 中,
中, ,则
,则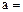 _______,
_______, ________。
________。