题目内容
已知函数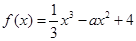 ,且
,且 是函数
是函数 的一个极小值点.
的一个极小值点.
(1)求实数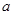 的值;
的值;
(2)求 在区间
在区间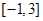 上的最大值和最小值.
上的最大值和最小值.
(1)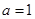 ;(2)当
;(2)当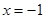 或
或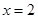 时,
时, 有最小值
有最小值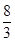 ;当
;当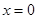 或
或 时,
时, 有最大值
有最大值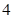 .
.
解析试题分析:(1)先求函数的导函数,因为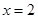 是函数
是函数 的一个极小值点,所以
的一个极小值点,所以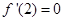 ,即可求得
,即可求得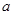 的值.(2)由(1)知,
的值.(2)由(1)知,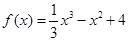 ,求导,在令导数等于0,讨论导数的正负可得函数的单调区间,根据函数的单调区间可求其最值.
,求导,在令导数等于0,讨论导数的正负可得函数的单调区间,根据函数的单调区间可求其最值.
试题解析:(1)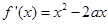 . 2分
. 2分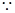
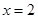 是函数
是函数 的一个极小值点,
的一个极小值点,
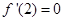 .
.
即 ,解得
,解得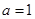 . 4分
. 4分
经检验,当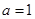 时,
时,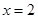 是函数
是函数 的一个极小值点.
的一个极小值点.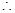 实数
实数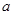 的值为
的值为 5分
5分
(2)由(1)知,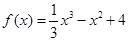 .
.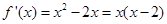 .
.
令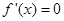 ,得
,得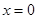 或
或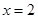 . 7分
. 7分
当 在
在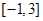 上变化时,
上变化时,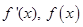 的变化情况如下:
的变化情况如下:
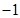
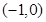

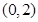
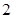
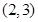

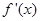


零负担作业系列答案
联动课堂课时作业系列答案
整合集训天天练系列答案

北斗星快乐夺冠系列答案
尖子班课时卷系列答案
世纪金榜高中全程学习方略系列答案


练习与测试系列答案
 的定义域是
的定义域是 ,其中常数
,其中常数 .(注:
.(注: 
 ,求
,求 的过原点的切线方程.
的过原点的切线方程. ,恒有
,恒有 .
. 时,求最大实数
时,求最大实数 ,使不等式
,使不等式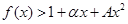 对
对 恒成立.
恒成立.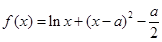 ,
,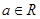 .
. 在
在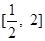 上单调递增,求实数
上单调递增,求实数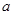 的取值范围;
的取值范围;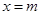 为函数
为函数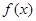 的图象与
的图象与 轴交于
轴交于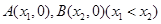 两点,且
两点,且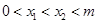 ,
,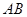 中点为
中点为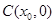 ,
,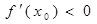 .
. .
. 处的切线为
处的切线为 ,求实数
,求实数 和
和 的值;
的值; ,曲线
,曲线 总在直线
总在直线 :
: 的上方,求实数
的上方,求实数 的取值范围.
的取值范围.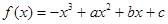 在
在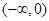 上是减函数,在
上是减函数,在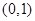 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且
上有三个零点,且 是其中一个零点.
是其中一个零点.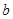 的值;
的值;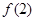 的取值范围;
的取值范围;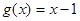 ,且
,且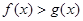 的解集为
的解集为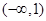 ,求实数
,求实数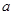 的取值范围.
的取值范围. ,且
,且 是函数
是函数 的一个极小值点.
的一个极小值点. 的值;
的值;  上的最大值和最小值.
上的最大值和最小值.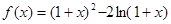
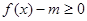 在
在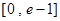 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;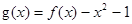 ,若关于x的方程
,若关于x的方程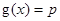 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.
 ,函数
,函数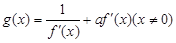
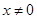 时,求函数
时,求函数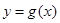 的表达式;
的表达式;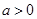 ,函数
,函数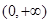 上的最小值是2 ,求
上的最小值是2 ,求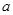 的值.
的值.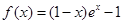 .
.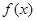 的最大值;
的最大值; ,
, ,且
,且 ,证明:
,证明: .
.