题目内容
（本小题满分12分）
如图，在
中，
是
上的高，沿
把折起，使
。
（Ⅰ）证明：平面ＡＤＢ ⊥平面ＢＤＣ；
（Ⅱ）设Ｅ为ＢＣ的中点，求
与
夹角的余弦值。
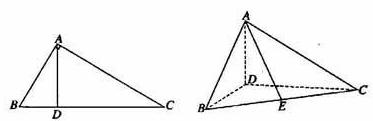
解（Ⅰ）∵折起前ＡＤ是ＢＣ边上的高，
∴ 当Δ ＡＢＤ折起后，AD⊥ＤＣ，AD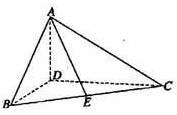⊥ＤＢ，
又DB
ＤＣ＝Ｄ，
∴ＡＤ⊥平面ＢＤＣ，
∵AD 平面
平面BDC．
平面ABD
平面BDC。
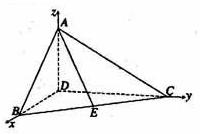（Ⅱ）由∠ ＢＤＣ＝
及（Ⅰ）知DA，ＤＢ，DC两两垂直，不防设
=1，以D为坐标原点，以
所在直线
轴建立如图所示的空间直角坐标系，易得D（0,0,0），B（1,0,0），C（0,3,0），A（0,0，
），E（
，
，0），
=
，
=（1，0,0,），
与夹角的余弦值为
＜
，＞=
．
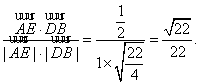
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
