题目内容
f(x)=|x-2|+x+1,若f(x)≥m对任意实数x恒成立,则实数m的取值范围是
- A.(-∞,3]
- B.[3,+∞)
- C.(-∞,2]
- D.[2,+∞)
A
分析:将函数解析式进行化简,然后求出其最小值,要使f(x)≥m对任意实数x恒成立,只需m≤f(x)min即可.
解答:f(x)=|x-2|+x+1=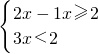
该函数的最小值为3
∵f(x)≥m对任意实数x恒成立
∴m≤f(x)min=3
故选A.
点评:本题主要考查了函数恒成立问题,以及函数的最值的求解,同时考查了转化的思想,属于基础题.
分析:将函数解析式进行化简,然后求出其最小值,要使f(x)≥m对任意实数x恒成立,只需m≤f(x)min即可.
解答:f(x)=|x-2|+x+1=
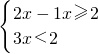
该函数的最小值为3
∵f(x)≥m对任意实数x恒成立
∴m≤f(x)min=3
故选A.
点评:本题主要考查了函数恒成立问题,以及函数的最值的求解,同时考查了转化的思想,属于基础题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
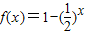 是[-1,0]上的一阶回归函数
是[-1,0]上的一阶回归函数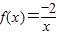 是(0,+∞)上的二阶回归函数;
是(0,+∞)上的二阶回归函数;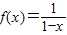 是(2,+∞)上的三阶回归函数.
是(2,+∞)上的三阶回归函数. 是[-1,0]上的一阶回归函数
是[-1,0]上的一阶回归函数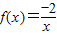 是(0,+∞)上的二阶回归函数;
是(0,+∞)上的二阶回归函数; 是(2,+∞)上的三阶回归函数.
是(2,+∞)上的三阶回归函数.