题目内容
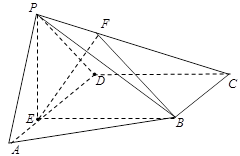
如图,四棱锥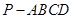 中,
中,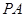 ⊥底面
⊥底面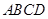 ,底面
,底面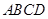 为菱形,点
为菱形,点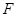 为侧棱
为侧棱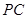 上一点.
上一点.
(1)若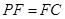 ,求证:
,求证: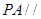 平面
平面 ;
;
(2)若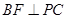 ,求证:平面
,求证:平面 ⊥平面
⊥平面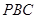 .
.
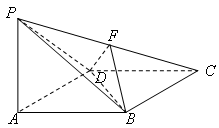
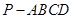 中,
中,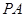 ⊥底面
⊥底面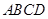 ,底面
,底面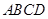 为菱形,点
为菱形,点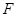 为侧棱
为侧棱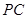 上一点.
上一点.(1)若
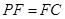 ,求证:
,求证: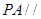 平面
平面 ;
; (2)若
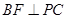 ,求证:平面
,求证:平面 ⊥平面
⊥平面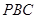 .
.
(1)详见解析; (2)详见解析
试题分析:(1) 要证证
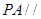 平面
平面 ,根据线面平行的判定定理可转化为线线平行,在本题中可取
,根据线面平行的判定定理可转化为线线平行,在本题中可取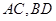 的交点为
的交点为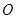 ,转化为证明
,转化为证明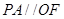 ,且
,且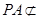 平面
平面 ,
,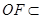 平面
平面 ,即可得证
,即可得证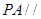 平面
平面 ;(2)要证平面
;(2)要证平面 ⊥平面
⊥平面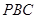 ,联想到面面垂直的判定定理,可转化为证线面垂直,由于底面
,联想到面面垂直的判定定理,可转化为证线面垂直,由于底面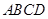 为菱形,则对角线
为菱形,则对角线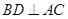 ,又
,又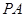 ⊥底面
⊥底面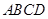 ,可得
,可得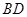 ⊥平面
⊥平面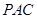 ,进而得到
,进而得到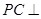 平面
平面 ,再加之
,再加之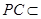 平面
平面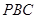 ,即可证得平面
,即可证得平面 ⊥平面
⊥平面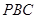 .
.(1) 证:(1)设
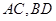 的交点为
的交点为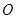 ,连
,连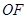
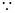 底面
底面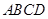 为菱形,
为菱形,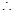
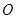 为
为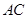 中点,
中点,又
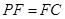 ,
,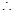
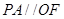 , 5分
, 5分且
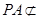 平面
平面 ,
,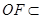 平面
平面 ,
,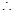
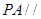 平面
平面 . 7分
. 7分(2)
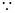 底面
底面 为菱形,
为菱形,
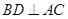 ,
,
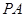 ⊥底面
⊥底面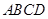 ,
,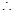
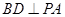 ,
,
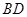 ⊥平面
⊥平面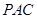 ,
,
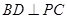 ,
,
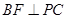 ,
,
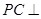 平面
平面 ,
,又
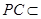 平面
平面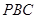 ,
,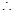 平面
平面 ⊥平面
⊥平面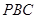 . 14分
. 14分
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 CD=1,PD=
CD=1,PD= .
.
 ?
?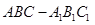 中,点
中,点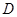 在边
在边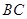 上,
上,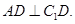
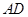
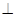 平面
平面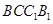 ;
; 是
是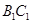 的中点,求证:
的中点,求证: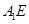 //平面
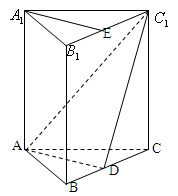
//平面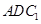 .
.
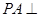 平面ABCD,AD//BC,
平面ABCD,AD//BC,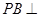 AC,
AC,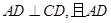
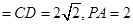 ,点M在线段PD上.
,点M在线段PD上.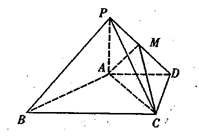
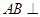 平面PAC;
平面PAC;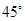 ,试确定点M的位置.
,试确定点M的位置. 中,
中, ,
, ,点
,点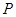 为
为 的中点。
的中点。
 ∥平面
∥平面 ;
; 平面
平面 ;
;
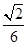 ,求线段AM的长.
,求线段AM的长.
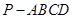 中,
中,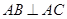 ,
,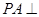 平面
平面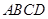 ,且
,且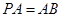 ,点
,点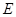 是
是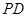 的中点.
的中点.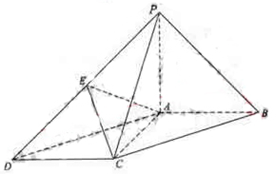
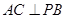 ;
;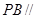 平面
平面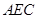 ;
;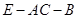 的大小.
的大小. 中,
中, 为
为 上一点,面
上一点,面 面
面 ,四边形
,四边形 为矩形
为矩形 ,
, ,
,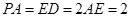 .
.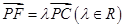 ,且
,且 ∥面
∥面 ,求
,求 的值;
的值; 面
面 ,并求点
,并求点 到面
到面 的距离.
的距离.