题目内容
已知向量a＝（3sinα，cosα），b＝(2sinα,
5sinα－4cosα)，α∈（
），且a⊥b．
（1）、求tanα的值；
（2）、求cos(
)的值．
【答案】
解：（1）∵a⊥b，∴a·b＝0．而a＝（3sinα，cosα），b＝(2sinα, 5sinα－4cosα)，
故a·b＝6sin2α＋5sinαcosα－4cos2α＝0．……………………………………2分
由于cosα≠0，∴6tan2α＋5tanα－4 ＝0．解之，得tanα＝－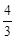
，或tanα＝
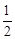．6分
∵α∈（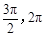
），tanα＜0，故tanα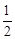＝（舍去）．∴tanα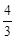＝－．…………7分
（2）∵α∈（），∴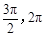
．
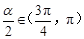由tanα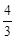＝－，求得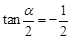
，
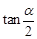＝2（舍去）．
∴
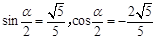，……………………………………………………12分
cos(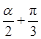
)＝
＝
＝
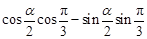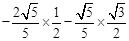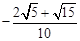．……14分
【解析】略
练习册系列答案
相关题目
），且a⊥b． 求tanα的值；
），且a⊥b． 
)的值．
），且a⊥b． 
)的值．
），且a⊥b． 
)的值．