Question

【题目】如图，在斜三棱柱中，侧面与侧面都是菱形，，．

求证：；

若，求二面角的余弦值．

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）－．

【解析】

试题分析：（Ⅰ）要证明线线垂直，一般要证线面垂直，因此要证线线垂直，题中只有两个60°角的菱形，因此有等边三角形，只要取中点为，则有CC1⊥OA，CC1⊥OB1，因此有线面垂直，从而证得题中的线线垂直；（Ⅱ）要求二面角，由己知又可得，因此以OB1，OC1，OA为正方向建立空间直角坐标系，可写出各点坐标，从而求得两平面CAB1和平面A1AB1的法向量，由法向量夹角余弦得二面角余弦，要注意二面角是锐角还是钝角．

试题解析：（Ⅰ）证明：连AC1，CB1，则

△ACC1和△B1CC1皆为正三角形．

取CC1中点O，连OA，OB1，则

CC1⊥OA，CC1⊥OB1，则

CC1⊥平面OAB1，则CC1⊥AB1． …4分

（Ⅱ）解：由（Ⅰ）知，OA＝OB1＝，又AB1＝，

所以OA⊥OB1．如图所示，分别以OB1，OC1，OA为正方向建立空间直角坐标系，

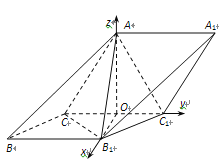
则C(0，－1，0)，B1(，0，0)，A(0，0，)，

设平面CAB1的法向量为m＝(x1，y1，z1)， 因为＝(，0，－)，＝(0，－1，－)，

所以取m＝(1，－，1)．

设平面A1AB1的法向量为n＝(x2，y2，z2)， 因为＝(，0，－)，＝ (0，2，0)，

所以取n＝(1，0，1)．

则cosm，n＝＝＝，因为二面角C-AB1-A1为钝角，

所以二面角C-AB1-A1的余弦值为－．