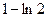题目内容
(本题满分12分)已知函数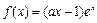 ,
,
(I)当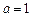 时,求函数
时,求函数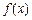 的极值;
的极值;
(II)若函数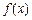 在区间
在区间 上是单调增函数,求实数
上是单调增函数,求实数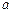 的取值范围.
的取值范围.
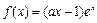 ,
,
(I)当
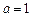 时,求函数
时,求函数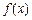 的极值;
的极值; (II)若函数
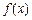 在区间
在区间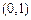 上是单调增函数,求实数
上是单调增函数,求实数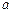 的取值范围.
的取值范围.(I)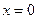 时,
时,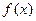 取得极小值
取得极小值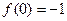 .
.
(II)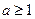
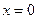 时,
时,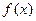 取得极小值
取得极小值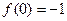 .
.(II)
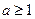
解:(I)因为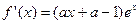 ,所以当
,所以当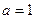 时,
时, ,
,
令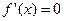 ,则
,则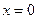 ,所以
,所以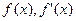 的变化情况如下表:
的变化情况如下表:
所以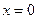 时,
时,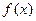 取得极小值
取得极小值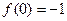 . …………………………………6分
. …………………………………6分
(II) 因为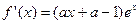 ,函数
,函数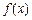 在区间
在区间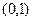 上是单调增函数,
上是单调增函数,
所以 对
对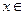
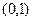 恒成立.又
恒成立.又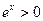 ,所以只要
,所以只要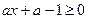 对
对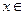
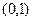 恒成立, 解法一:设
恒成立, 解法一:设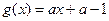 ,则要使
,则要使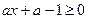 对
对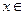
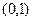 恒成立,
恒成立,
只要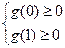 成立,即
成立,即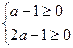 ,解得
,解得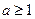 .
.
解法二:要使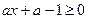 对
对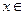
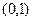 恒成立,
恒成立,
因为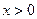 ,所以
,所以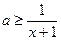 对
对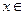
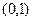 恒成立,
恒成立,
因为函数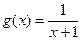 在
在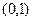 上单调递减,
上单调递减,
所以只要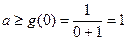 .
.
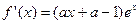 ,所以当
,所以当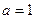 时,
时, ,
,令
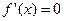 ,则
,则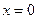 ,所以
,所以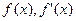 的变化情况如下表:
的变化情况如下表: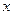 | 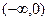 | 0 | 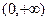 |
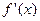 | 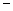 | 0 | + |
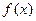 | 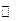 | 极小值 | 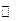 |
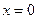 时,
时,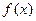 取得极小值
取得极小值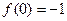 . …………………………………6分
. …………………………………6分(II) 因为
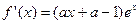 ,函数
,函数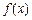 在区间
在区间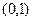 上是单调增函数,
上是单调增函数,所以
 对
对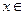
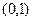 恒成立.又
恒成立.又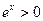 ,所以只要
,所以只要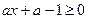 对
对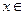
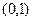 恒成立, 解法一:设
恒成立, 解法一:设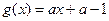 ,则要使
,则要使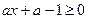 对
对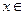
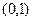 恒成立,
恒成立,只要
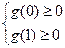 成立,即
成立,即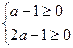 ,解得
,解得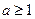 .
. 解法二:要使
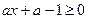 对
对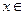
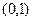 恒成立,
恒成立,因为
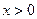 ,所以
,所以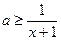 对
对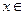
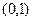 恒成立,
恒成立, 因为函数
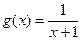 在
在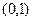 上单调递减,
上单调递减, 所以只要
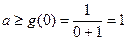 .
. 
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
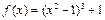 的极值是 ( )
的极值是 ( )
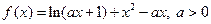 ,
,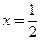 是函数
是函数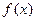 的一个极值点,求
的一个极值点,求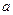 ;
;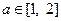 ,不等式
,不等式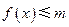 在
在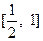 上恒成立,求
上恒成立,求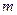 的取值范围.
的取值范围.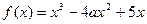 (
(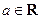 ).
).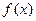 在区间[0, 2]上无极值, 求a的取值范围.
在区间[0, 2]上无极值, 求a的取值范围.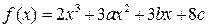 在
在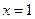 及
及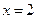 时取得极值,
时取得极值,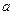 、
、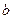 的值;
的值;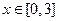 ,都有
,都有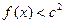 成立,求c的取值范围.
成立,求c的取值范围.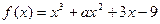 ,已知
,已知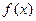 在
在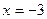 时取得极值,则
时取得极值,则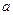 = ▲ .
= ▲ .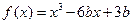 在
在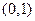 内有极小值,则实数b的取值范围是( )
内有极小值,则实数b的取值范围是( )



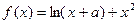
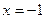 时,
时,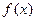 取得极值,求
取得极值,求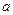 值,并讨论
值,并讨论