题目内容
已知| |=3,|
|=3,| |=1,且
|=1,且 与
与 同向共线,则
同向共线,则 •
• 的值是
的值是
- A.-3
- B.0
- C.3
- D.-3或3
C
分析:本题考查的知识点是平面向量的数量积运算,由 与
与 同向共线,则
同向共线,则 与
与 夹角为0,代入平面向量的数量积公式易得结果.
夹角为0,代入平面向量的数量积公式易得结果.
解答:∵ 与
与 同向共线,
同向共线,
∴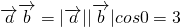 ,
,
故选C.
点评:如果两个非量平面向量平行(共线),则它们的方向相同或相反,此时他们的夹角为0或π.当它们同向时,夹角为0,此时向量的数量积,等于他们模的积;当它们反向时,夹角为π,此时向量的数量积,等于他们模的积的相反数.如果两个向量垂直,则它们的夹角为 ,此时向量的数量积,等于0.
,此时向量的数量积,等于0.
分析:本题考查的知识点是平面向量的数量积运算,由
 与
与 同向共线,则
同向共线,则 与
与 夹角为0,代入平面向量的数量积公式易得结果.
夹角为0,代入平面向量的数量积公式易得结果.解答:∵
 与
与 同向共线,
同向共线,∴
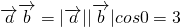 ,
,故选C.
点评:如果两个非量平面向量平行(共线),则它们的方向相同或相反,此时他们的夹角为0或π.当它们同向时,夹角为0,此时向量的数量积,等于他们模的积;当它们反向时,夹角为π,此时向量的数量积,等于他们模的积的相反数.如果两个向量垂直,则它们的夹角为
 ,此时向量的数量积,等于0.
,此时向量的数量积,等于0. 
练习册系列答案
相关题目
已知
<α<π,tanα+cotα=-
,则tanα的值为( )
| 3π |
| 4 |
| 10 |
| 3 |
| A、-3 | ||
B、-
| ||
C、-3或-
| ||
D、-
|