题目内容
已知α=| π |
| 3 |
(1)写出所有与α终边相同的角;
(2)写出在(-4π,2π)内与α终边相同的角;
(3)若角β与α终边相同,则
| β |
| 2 |
分析:(1)有与α终边相同的角可以写成2kπ+α,k∈Z.
(2)令-4π<2kπ+
<2π(k∈Z),解出整数k,从而求得在(-4π,2π)内与α终边相同的角.
(3)根据β=2kπ+
(k∈Z),求得
=kπ+
(k∈Z),即可判断
是第几象限的角.
(2)令-4π<2kπ+
| π |
| 3 |
(3)根据β=2kπ+
| π |
| 3 |
| β |
| 2 |
| π |
| 6 |
| β |
| 2 |
解答:解:(1)所有与α终边相同的角可表示为
{θ|θ=2kπ+
,k∈Z}.
(2)由(1)令-4π<2kπ+
<2π(k∈Z),则有
-2-
<k<1-
.
又∵k∈Z,∴取k=-2,-1,0.
故在(-4π,2π)内与α终边相同的角是-
、-
、
.
(3)由(1)有β=2kπ+
(k∈Z),则
=kπ+
(k∈Z),当k为偶数时,
在第一象限,
当k为奇数时,
在第三象限.
∴
是第一、三象限的角.
{θ|θ=2kπ+
| π |
| 3 |
(2)由(1)令-4π<2kπ+
| π |
| 3 |
-2-
| 1 |
| 6 |
| 1 |
| 6 |
又∵k∈Z,∴取k=-2,-1,0.
故在(-4π,2π)内与α终边相同的角是-
| 11π |
| 3 |
| 5π |
| 3 |
| π |
| 3 |
(3)由(1)有β=2kπ+
| π |
| 3 |
| β |
| 2 |
| π |
| 6 |
| β |
| 2 |
当k为奇数时,
| β |
| 2 |
∴
| β |
| 2 |
点评:本题考查终边相同的角的表示方法,及一元一次不等式的解法,体现了分类讨论的数学思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
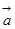 ={3λ,6, λ+6},
={3λ,6, λ+6}, 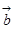 ={λ+1,3,2λ},若
={λ+1,3,2λ},若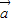 |=3,
|=3,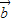 =(1,2),且
=(1,2),且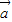 ∥
∥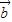 ,则
,则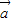 的坐标为( )
的坐标为( )