题目内容
【题目】如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.
(Ⅰ)求证:CD⊥A′B;
(Ⅱ)试在线段A′C上确定一点P,使得二面角P﹣BD﹣C的大小为45°.
【答案】证明:(I)证法一:在△ABC中,由余弦定理得BD2=AB2+AD2﹣2ABADcosA=4+4+8cosC,
在△BCD中,由余弦定理得BD2=BC2+CD2﹣2BCCDcosC=16+4﹣16cosC
由上述两式可知, ![]()
∴BD⊥CD
又∵面A'BD⊥面CBD,面A'BD∩面CBD=BD,
∴CD⊥面A'BD
∵A'B面A'BD,∴A'B⊥CD.
(II)解:
法一:存在.P为A'C上靠近A'的三等分点.
取BD的中点O,连接A′O,∵A'B=A'D∴A'O⊥BD
又∵平面A′BD⊥平面CBD,∴A'O⊥平面CBD,
∴平面A'OC⊥平面BCD,
过点P作PQ⊥OC于Q,则PQ⊥平面BCD,过点Q作QH⊥BD于H,连接PH.
则QH是PH在平面BDC的射影,故PH⊥BD,
所以,∠PHQ为二面角P﹣BD﹣C的平面角,
P为A'C上靠近A'的三等分点,
∴ ![]() ,
, ![]() ,∴
,∴ ![]() ,∴∠PHD=45°.
,∴∠PHD=45°.
∴二面角P﹣BD﹣C的大小为45°.
证明:(Ⅰ)证法一:在等腰梯形ABCD中,过点A作AE⊥BC于E,
过点D作DF⊥BC于F,则AE∥DF,∴EF=AD=2,
又∵在等腰梯形ABCD中,Rt△ABE≌Rt△DCF且BC=4∴BE=FC=1∴ ![]() D
D
在△BCD中, ![]() ,
,
∴BD2+CD2=BC2 , ∴CD⊥BD,
又∵平面A'BD⊥平面CBD,
面A'BD∩面CBD=BD∴CD⊥平面A'BD∴CD⊥A'B.
(Ⅱ)解法二:由(Ⅰ)知CD⊥BD,CD⊥平面A′BD.
以D为坐标原点,以 ![]() 的方向为x轴正方向,建立如图所示的空间直角坐标系D﹣xyz.
的方向为x轴正方向,建立如图所示的空间直角坐标系D﹣xyz.
则D(0,0,0), ![]() ,C(0,2,0),
,C(0,2,0),
取BD的中点O,连接A'O,∵A'B=A'D∴A'O⊥BD
在等腰△A'BD中 ![]() 可求得A'O=1∴
可求得A'O=1∴ ![]()
所以 ![]() ,
, ![]()
设 ![]() ,则
,则 ![]()
设 ![]() 是平面PBD的法向量,则
是平面PBD的法向量,则  ,
,
即 ![]() 可取
可取 ![]()
易知:平面CBD的一个法向量为 ![]()
由已知二面角P﹣BD﹣C的大小为45°.
∴  ,
,
解得: ![]() 或λ=﹣1(舍)
或λ=﹣1(舍)
∴点P在线段A'C靠近A'的三等分点处.
【解析】(I)法一:由余弦定理推导出BD⊥CD,从而CD⊥面A'BD,由此能证明A'B⊥CD.
法二:过点A作AE⊥BC于E,过点D作DF⊥BC于F,则AE∥DF,推导出CD⊥BD,从而CD⊥平面A'BD,由此能证明CD⊥A'B.(II)法一:取BD的中点O,连接A′O,推导出平面A'OC⊥平面BCD,过点P作PQ⊥OC于Q,则PQ⊥平面BCD,过点Q作QH⊥BD于H,连接PH,推导出PH⊥BD,从而∠PHQ为二面角P﹣BD﹣C的平面角,由此能求出P为A'C上靠近A'的三等分点,二面角P﹣BD﹣C的大小为45°.
法二:以D为坐标原点,以 ![]() 的方向为x轴正方向,建立空间直角坐标系D﹣xyz,利用向量法能求出点P在线段A'C靠近A'的三等分点处.
的方向为x轴正方向,建立空间直角坐标系D﹣xyz,利用向量法能求出点P在线段A'C靠近A'的三等分点处.
【考点精析】根据题目的已知条件,利用直线与平面垂直的性质的相关知识可以得到问题的答案,需要掌握垂直于同一个平面的两条直线平行.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】下表是某地一家超市在2018年一月份某一周内周2到周6的时间![]() 与每天获得的利润
与每天获得的利润![]() (单位:万元)的有关数据.
(单位:万元)的有关数据.
星期 | 星期2 | 星期3 | 星期4 | 星期5 | 星期6 |
利润 | 2 | 3 | 5 | 6 | 9 |
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(2)估计星期日获得的利润为多少万元.
参考公式: 
【题目】某汽车公司对最近6个月内的市场占有率进行了统计,结果如表;
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)可用线性回归模型拟合![]() 与
与![]() 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购![]() 两款车扩大市场,
两款车扩大市场, ![]() 两款车各100辆的资料如表:
两款车各100辆的资料如表:
车型 | 报废年限(年) | 合计 | 成本 | |||
1 | 2 | 3 | 4 | |||
| 10 | 30 | 40 | 20 | 100 | 1000元/辆 |
| 15 | 40 | 35 | 10 | 100 | 800元/辆 |
平均每辆车每年可为公司带来收入![]() 元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数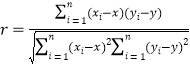 ;
;
回归直线方程为![]() ,其中
,其中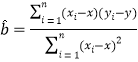 ,
,![]() .
.


