题目内容

在空间四边形OABC中，OA=8，AB=6，AC=4，BC=5，∠OAC=45°，∠OAB=60°．则异面直线AO与BC的夹角的余弦值为
1
5
(3-2
2
)
1
5
(3-2
2
)
．
分析：根据已给条件该题可利用数量积的方法求解．要求OA与BC夹角的余弦值，可求
OA
与
BC
的夹角的余弦值，利用
BC
=
BA
+
AC
 代入向量的夹角公式求解即可．
解答：解：∵
OA
•
BA
=8×6cos60°=24
       
OA
•
AC
=8×4cos135°=-16
2

∴设异面直线AO与BC的夹角为θ则cosθ=
OA
•
BC
|
OA
||
BC
|
=
OA
•(
BA
+
AC
)
|
OA
||
BC
|
=
24-16
2
8×5
=
3-2
2
5

所以OA与BC夹角的余弦值为
3-2
2
5
点评：本题主要考查了利用向量的数量积求异面直线及其所成的角，属有一定难度的基础题．解题的关键是将异面直线AO与BC的夹角转化为求
OA
与
BC
的夹角！
练习册系列答案
相关题目
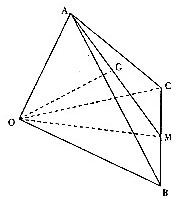精英家教网如图，在空间四边形OABC中，M，G分别是BC，AM的中点，设
OA
=
a
，
OB
=
b
，
OC
=
c
．
（1）用基底{
a
 ， 
b
 ，
c
}表示向量
OG
；
（2）若|
a
|=|
b
|=|
c
|=
3
，且
a
与
b
、
c
夹角的余弦值均为
1
3
，
b
与
c
夹角为60°，求|
OG
|．
在空间四边形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在线段OA上，且OM=2MA，N为BC的中点，则
MN
等于（　　）
（理科试题）如图，在空间四边形OABC中，G是△ABC的重心，若
OG
=x
OA
+y
OB
+z
OC
，则x+y+z=
1
1
．
如图，在空间四边形OABC中，已知E是线段BC的中点，G为AE的中点，若
OA
，
OB
，
OC
分别记为
a
，
b
，
c
，则用
a
，
b
，
c
表示
OG
的结果为
OG
=
1
2
a
+
1
4
b
+
1
4
c
1
2
a
+
1
4
b
+
1
4
c
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网