题目内容
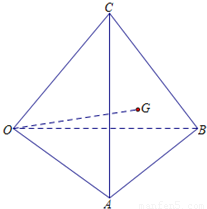
 (理科试题)如图,在空间四边形OABC中,G是△ABC的重心,若
(理科试题)如图,在空间四边形OABC中,G是△ABC的重心,若| OG |
| OA |
| OB |
| OC |
1
1
.分析:取AB中点D,连接OD、CD,根据G是△ABC的重心,得到
=2
,所以
=
+
…①;因为D为线段AB中点,所以
=
+
…②,①②联解得
=
+
+
.由此结合题意,得x=y=z=
,可得x+y+z=1.
| CG |
| GD |
| OG |
| 1 |
| 3 |
| OC |
| 2 |
| 3 |
| OD |
| OD |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| OG |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| 1 |
| 3 |
解答:解: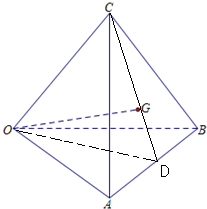 取AB中点D,连接OD、CD,因为G是△ABC的重心,所以G在CD上且CG=2GD
取AB中点D,连接OD、CD,因为G是△ABC的重心,所以G在CD上且CG=2GD
∵
=2
,即
-
=2(
-
)
∴
=
+
…①
又∵D为线段AB中点
∴
=
+
…②,
将②代入①得
=
+
(
+
)=
+
+
.
∵
=x
+y
+z
,
∴x=y=z=
,可得x+y+z=1
故答案为:1
 取AB中点D,连接OD、CD,因为G是△ABC的重心,所以G在CD上且CG=2GD
取AB中点D,连接OD、CD,因为G是△ABC的重心,所以G在CD上且CG=2GD∵
| CG |
| GD |
| OG |
| OC |
| OD |
| OG |
∴
| OG |
| 1 |
| 3 |
| OC |
| 2 |
| 3 |
| OD |
又∵D为线段AB中点
∴
| OD |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
将②代入①得
| OG |
| 1 |
| 3 |
| OC |
| 2 |
| 3 |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
∵
| OG |
| OA |
| OB |
| OC |
∴x=y=z=
| 1 |
| 3 |
故答案为:1
点评:本题在四面体中,由一顶点指向对面三角形重心的向量为例,考查了空间向量基本定理及其应用,属于基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
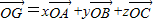 ,则x+y+z= .
,则x+y+z= .