题目内容
在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围图形的面积为
.试求切点A的坐标及过切点A的切线方程.

| 1 |
| 12 |

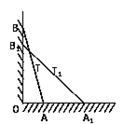
如图所示,设切点A(x0,y0),
由y′=2x,得过点A的切线方程为
y-y0=2x0(x-x0),即y=2x0x-x02.
令y=0,得x=
,即C(
,0).
设由曲线和过A点的切线及x轴所围成图形的面积为S.
S曲边三角形AOB=∫x00x2dx=
x3|x00=
x03,
S△ABC=
|BC|•|AB|=
(x0-
)•x02=
x03.
∴S=
x03-
x03=
x03=
.
∴x0=1,从而切点A的坐标为(1,1),切线方程为y=2x-1.

由y′=2x,得过点A的切线方程为
y-y0=2x0(x-x0),即y=2x0x-x02.
令y=0,得x=
| x0 |
| 2 |
| x0 |
| 2 |
设由曲线和过A点的切线及x轴所围成图形的面积为S.
S曲边三角形AOB=∫x00x2dx=
| 1 |
| 3 |
| 1 |
| 3 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| x0 |
| 2 |
| 1 |
| 4 |
∴S=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 12 |
∴x0=1,从而切点A的坐标为(1,1),切线方程为y=2x-1.


练习册系列答案
相关题目
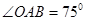 ,当竹竿滑动到A1B1位置时,
,当竹竿滑动到A1B1位置时,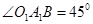 ,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.
,竹竿在滑动时中点T也沿着某种轨迹运动到T1点,则T运动的路程是_________米.