题目内容
设奇函数f(x)在[－1,1]上是增函数，且f(－1)＝－1，若函数f(x)≤t2－2at＋1对所有的x∈[－1,1]都成立，则当a∈[－1,1]时t的取值范围是( )．
A．－2≤t≤2 B．－
≤t≤
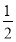
C．t≤－2或t＝0或t≥2 D．t≤－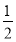
或t＝0或t≥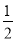
C
【解析】依题意f(x)的最大值为f(1)＝1，要使f(x)≤t2－2at＋1对所有的x∈[－1,1]都成立，则1≤t2－2at＋1，即t2－2at≥0，亦即t(t－2a)≥0，当t＝0时，不等式成立，当0≤a≤1时，不等式的解为t≥2a≥2；当－1≤a≤0时，不等式的解为t≤2a≤－2.
练习册系列答案
计算高手系列答案
相关题目
受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：
品牌 | 甲 | 乙 | |||
首次出现故 障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
每辆利润 (万元) | 1 | 2 | 3 | 1.8 | 2.9 |
将频率视为概率，解答下列问题：
(1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率．
(2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列．
(3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．