题目内容
下列命题中:①若函数f(x)的定义域为R,则g(x)=f(x)+f(-x)一定是偶函数;
②直线x=
| π |
| 2 |
| π |
| 2 |
③若1,a,b,c,4这五个数组成一个等比数列,则b=±2;
④若实数x,y满足
|
其中正确的命题序号是
分析:根据偶函数的定义,可以判断①的真假;根据正弦型函数的对称性,我们可以判断②的真假;根据等比数列奇数(偶数)项符号相同,可以判断③的真假;根据简单线性规划,我们求出目标函数Z=x+y的最大值,可判断④的真假,进而得到答案.
解答:解:∵g(-x)=f(-x)+f(x)=g(x),故①为真命题;
当x=
时,y=sin(2x-
)取最大值1,根据正弦型函数的对称性,可得②为真命题;
若1,a,b,c,4这五个数组成一个等比数列,则b>0,且b2=4,故b=2,即③为假命题;
若实数x,y满足
,则当x=2,y=2时,x+y的最大值是4,即④为假命题;
故答案为:①②
当x=
| π |
| 2 |
| π |
| 2 |
若1,a,b,c,4这五个数组成一个等比数列,则b>0,且b2=4,故b=2,即③为假命题;
若实数x,y满足
|
故答案为:①②
点评:本题考查的知识点是命题的真假判断与应用,函数奇偶性的判断,简单线性规划,正弦型函数的对称性,其中③中,易忽略等比数列奇数(偶数)项符号相同,而错认为是正确的,而将本题错解为①②③.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足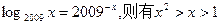 成立;
成立; 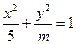 的离心率
的离心率 ,则
,则 的值为3;
的值为3; 若
若 则函数在
则函数在 内至多有一零点;
内至多有一零点; 与
与 的图像关于直线
的图像关于直线 对称;
对称; .
.