题目内容
(2013•福建)将函数f(x)=sin(2x+θ)(-
<θ<
)的图象向右平移φ({φ>1})个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P(0,
),则φ的值可以是( )
| π |
| 2 |
| π |
| 2 |
| ||
| 2 |
分析:求出平移后的函数解析式,利用两个函数都经过P(0,
),解出θ,然后求出φ即可.
| ||
| 2 |
解答:解:函数f(x)=sin(2x+θ)(-
<θ<
)向右平移φ个单位,得到g(x)=sin(2x+θ-2φ),
因为两个函数都经过P(0,
),所以sinθ=
(-
<θ<
),θ=
,
所以g(x)=sin(2x+
-2φ),sin(
-2φ)=
,φ>1,所以
-2φ=2kπ+
,φ=-kπ,与选项不符舍去,
-2φ=2kπ+
,k∈Z,当k=-1时,φ=
.
故选B.
| π |
| 2 |
| π |
| 2 |
因为两个函数都经过P(0,
| ||
| 2 |
| ||
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
所以g(x)=sin(2x+
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 5π |
| 6 |
故选B.
点评:本题考查函数图象的平移,函数值的求法,考查分析问题解决问题的能力与计算能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目

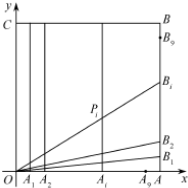 (2013•福建)如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点
(2013•福建)如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点 (2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)