题目内容
(2013•福建)已知函数f(x)=sin(wx+φ)(w>0,0<φ<π)的周期为π,图象的一个对称中心为(
,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
单位长度后得到函数g(x)的图象.
(1)求函数f(x)与g(x)的解析式
(2)是否存在x0∈(
,
),使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数,若不存在,说明理由;
(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点.
| π |
| 4 |
| π |
| 2 |
(1)求函数f(x)与g(x)的解析式
(2)是否存在x0∈(
| π |
| 6 |
| π |
| 4 |
(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点.
分析:(1)依题意,可求得ω=2,φ=
,利用三角函数的图象变换可求得g(x)=sinx;
(2)依题意,当x∈(
,
)时,
<sinx<
,0<cosx<
⇒sinx>cos2x>sinxcos2x,问题转化为方程2cos2x=sinx+sinxcos2x在(
,
)内是否有解.通过G′(x)>0,可知G(x)在(
,
)内单调递增,而G(
)<0,G(
)>0,从而可得答案;
(3)依题意,F(x)=asinx+cos2x,令F(x)=asinx+cos2x=0,方程F(x)=0等价于关于x的方程a=-
,x≠kπ(k∈Z).问题转化为研究直线y=a与曲线y=h(x),x∈(0,π)∪(π,2π)的交点情况.通过其导数,列表分析即可求得答案.
| π |
| 2 |
(2)依题意,当x∈(
| π |
| 6 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
(3)依题意,F(x)=asinx+cos2x,令F(x)=asinx+cos2x=0,方程F(x)=0等价于关于x的方程a=-
| cos2x |
| sinx |
解答:解:(1)∵函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的周期为π,
∴ω=
=2,
又曲线y=f(x)的一个对称中心为(
,0),φ∈(0,π),
故f(
)=sin(2×
+φ)=0,得φ=
,所以f(x)=cos2x.
将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cosx的图象,
再将y=cosx的图象向右平移
个单位长度后得到函数g(x)=cos(x-
)的图象,
∴g(x)=sinx.
(2)当x∈(
,
)时,
<sinx<
,0<cosx<
,
∴sinx>cos2x>sinxcos2x,
问题转化为方程2cos2x=sinx+sinxcos2x在(
,
)内是否有解.
设G(x)=sinx+sinxcos2x-cos2x,x∈(
,
),
则G′(x)=cosx+cosxcos2x+2sin2x(2-sinx),
∵x∈(
,
),
∴G′(x)>0,G(x)在(
,
)内单调递增,
又G(
)=-
<0,G(
)=
>0,且G(x)的图象连续不断,故可知函数G(x)在(
,
)内存在唯一零点x0,即存在唯一零点x0∈(
,
)满足题意.
(3)依题意,F(x)=asinx+cos2x,令F(x)=asinx+cos2x=0,
当sinx=0,即x=kπ(k∈Z)时,cos2x=1,从而x=kπ(k∈Z)不是方程F(x)=0的解,
∴方程F(x)=0等价于关于x的方程a=-
,x≠kπ(k∈Z).
现研究x∈(0,π)∪(π,2π)时方程a=-
的解的情况.
令h(x)=-
,x∈(0,π)∪(π,2π),
则问题转化为研究直线y=a与曲线y=h(x),x∈(0,π)∪(π,2π)的交点情况.
h′(x)=
,令h′(x)=0,得x=
或x=
,
当x变换时,h′(x),h(x)的变化情况如下表:
当x>0且x趋近于0时,h(x)趋向于-∞,
当x<π且x趋近于π时,h(x)趋向于-∞,
当x>π且x趋近于π时,h(x)趋向于+∞,
当x<2π且x趋近于2π时,h(x)趋向于+∞,
故当a>1时,直线y=a与曲线y=h(x)在(0,π)内无交点,在(π,2π)内有2个交点;
当a<-1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内无交点;
当-1<a<1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内有2个交点;
由函数h(x)的周期性,可知当a≠±1时,直线y=a与曲线y=h(x)在(0,nπ)内总有偶数个交点,从而不存在正整数n,使得直线y=a与曲线y=h(x)在(0,nπ)内恰有2013个零点;
又当a=1或a=-1时,直线y=a与曲线y=h(x)在(0,π)∪(π,2π)内有3个交点,由周期性,2013=3×671,
∴依题意得n=671×2=1342.
综上,当a=1,n=1342,或a=-1,n=1342时,函数F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点.
∴ω=
| 2π |
| T |
又曲线y=f(x)的一个对称中心为(
| π |
| 4 |
故f(
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cosx的图象,
再将y=cosx的图象向右平移
| π |
| 2 |
| π |
| 2 |
∴g(x)=sinx.
(2)当x∈(
| π |
| 6 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴sinx>cos2x>sinxcos2x,
问题转化为方程2cos2x=sinx+sinxcos2x在(
| π |
| 6 |
| π |
| 4 |
设G(x)=sinx+sinxcos2x-cos2x,x∈(
| π |
| 6 |
| π |
| 4 |
则G′(x)=cosx+cosxcos2x+2sin2x(2-sinx),
∵x∈(
| π |
| 6 |
| π |
| 4 |
∴G′(x)>0,G(x)在(
| π |
| 6 |
| π |
| 4 |
又G(
| π |
| 6 |
| 1 |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
(3)依题意,F(x)=asinx+cos2x,令F(x)=asinx+cos2x=0,
当sinx=0,即x=kπ(k∈Z)时,cos2x=1,从而x=kπ(k∈Z)不是方程F(x)=0的解,
∴方程F(x)=0等价于关于x的方程a=-
| cos2x |
| sinx |
现研究x∈(0,π)∪(π,2π)时方程a=-
| cos2x |
| sinx |
令h(x)=-
| cos2x |
| sinx |
则问题转化为研究直线y=a与曲线y=h(x),x∈(0,π)∪(π,2π)的交点情况.
h′(x)=
| cosx(2sin2x+1) |
| sin2x |
| π |
| 2 |
| 3π |
| 2 |
当x变换时,h′(x),h(x)的变化情况如下表:
| x | (0,
|
|
(
|
(π,
|
|
(
| ||||||||||||
| h′(x) | + | 0 | - | - | 0 | + | ||||||||||||
| h(x) | ↗ | 1 | ↘ | ↘ | -1 | ↗ |
当x<π且x趋近于π时,h(x)趋向于-∞,
当x>π且x趋近于π时,h(x)趋向于+∞,
当x<2π且x趋近于2π时,h(x)趋向于+∞,
故当a>1时,直线y=a与曲线y=h(x)在(0,π)内无交点,在(π,2π)内有2个交点;
当a<-1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内无交点;
当-1<a<1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内有2个交点;
由函数h(x)的周期性,可知当a≠±1时,直线y=a与曲线y=h(x)在(0,nπ)内总有偶数个交点,从而不存在正整数n,使得直线y=a与曲线y=h(x)在(0,nπ)内恰有2013个零点;
又当a=1或a=-1时,直线y=a与曲线y=h(x)在(0,π)∪(π,2π)内有3个交点,由周期性,2013=3×671,
∴依题意得n=671×2=1342.
综上,当a=1,n=1342,或a=-1,n=1342时,函数F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点.
点评:本题考查同角三角函数基本关系,三角恒等变换,三角函数的图象与性质,考查函数、函数的导数、函数的零点、不等式等基础知识,考查运算求解能力,抽象概括能力,推理论证能力,考查函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
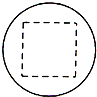 (2013•福建)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是
(2013•福建)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、俯视图、均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是