题目内容
已知函数f(x)=( )x,函数y=f-1(x)是函数y=f(x)的反函数.
)x,函数y=f-1(x)是函数y=f(x)的反函数.
(1)若函数y=f-1(mx2+mx+1)的定义域为R,求实数m的取值范围;
(2)当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a).
解:(1)∵f-1(x)
=log x(x>0),
x(x>0),
∴f-1(mx2+mx+1)
=log (mx2+mx+1),由题知,mx2+mx+1>0恒成立,
(mx2+mx+1),由题知,mx2+mx+1>0恒成立,
∴①当m=0时,1>0满足题意;
②当m≠0时,
应有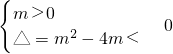
?0<m<4,
∴实数m的取值范围为
0≤m<4.
(2)∵x∈[-1,1],
∴( )x∈[
)x∈[ ,3],
,3],
y=[f(x)]2-2af(x)+3=[( )x]2-2a(
)x]2-2a( )x+3
)x+3
=[( )x-a]2+3-a2,
)x-a]2+3-a2,
当a< 时,
时,
ymin=g(a)= -
- ;
;
当 ≤a≤3时,
≤a≤3时,
ymin=g(a)=3-a2;
当a>3时,ymin=g(a)=12-6A、
∴g(a)=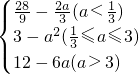
分析:(1)先求函数f(x)=( )x,的反函数,写出函数y=f-1(mx2+mx+1)的表达式,然后利用它的定义域为R,mx2+mx+1>0恒成立,求实数m的取值范围;
)x,的反函数,写出函数y=f-1(mx2+mx+1)的表达式,然后利用它的定义域为R,mx2+mx+1>0恒成立,求实数m的取值范围;
(2)求函数y=[f(x)]2-2af(x)+3的表达式,根据x∈[-1,1],求出( )x的范围,根据对称轴是否在(
)x的范围,根据对称轴是否在( )x的范围内求函数g(a)的最小值.
)x的范围内求函数g(a)的最小值.
点评:本题考查反函数,函数的最值及其几何意义,考查转化思想,恒成立问题,计算能力,以及分析问题解决问题的能力,是中档题.
=log
 x(x>0),
x(x>0),∴f-1(mx2+mx+1)
=log
 (mx2+mx+1),由题知,mx2+mx+1>0恒成立,
(mx2+mx+1),由题知,mx2+mx+1>0恒成立,∴①当m=0时,1>0满足题意;
②当m≠0时,
应有
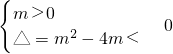
?0<m<4,
∴实数m的取值范围为
0≤m<4.
(2)∵x∈[-1,1],
∴(
 )x∈[
)x∈[ ,3],
,3],y=[f(x)]2-2af(x)+3=[(
 )x]2-2a(
)x]2-2a( )x+3
)x+3=[(
 )x-a]2+3-a2,
)x-a]2+3-a2,当a<
 时,
时,ymin=g(a)=
 -
- ;
;当
 ≤a≤3时,
≤a≤3时,ymin=g(a)=3-a2;
当a>3时,ymin=g(a)=12-6A、
∴g(a)=
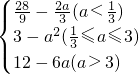
分析:(1)先求函数f(x)=(
 )x,的反函数,写出函数y=f-1(mx2+mx+1)的表达式,然后利用它的定义域为R,mx2+mx+1>0恒成立,求实数m的取值范围;
)x,的反函数,写出函数y=f-1(mx2+mx+1)的表达式,然后利用它的定义域为R,mx2+mx+1>0恒成立,求实数m的取值范围;(2)求函数y=[f(x)]2-2af(x)+3的表达式,根据x∈[-1,1],求出(
 )x的范围,根据对称轴是否在(
)x的范围,根据对称轴是否在( )x的范围内求函数g(a)的最小值.
)x的范围内求函数g(a)的最小值.点评:本题考查反函数,函数的最值及其几何意义,考查转化思想,恒成立问题,计算能力,以及分析问题解决问题的能力,是中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|