题目内容
已知点P(x,y)是渐近线为2x±3y=0且经过定点(6,2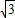 )的双曲线C1上的一动点,点Q是P关于双曲线C1实轴A1A2的对称点,设直线PA1与QA2的交点为M(x,y),
)的双曲线C1上的一动点,点Q是P关于双曲线C1实轴A1A2的对称点,设直线PA1与QA2的交点为M(x,y),(1)求双曲线C1的方程;
(2)求动点M的轨迹C2的方程;
(3)已知x轴上一定点N(1,0),过N点斜率不为0的直线L交C2于A、B两点,x轴上是否存在定点 K(x,0)使得∠AKN=∠BKN?若存在,求出点K的坐标;若不存在,说明理由.
【答案】分析:(1)直接设设c1方程为 4x2-9y2=λ,又点(6,2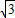 )在曲线上代入得λ=36即可得到结论;
)在曲线上代入得λ=36即可得到结论;
(2)结合已知得到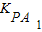 =
=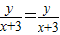 ,
,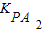 =
=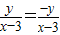 ;相乘整理即可得到结论;
;相乘整理即可得到结论;
(3)先联立直线方程与曲线方程,得到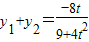 ,y1y2=
,y1y2=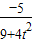 ;根据∠AKN=∠BKN得到KAN+KBN=0;整理后结合已知条件即可求出结论.
;根据∠AKN=∠BKN得到KAN+KBN=0;整理后结合已知条件即可求出结论.
解答:解:(1)可设c1方程为 4x2-9y2=λ,又点(6,2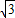 )在曲线上代入得λ=36.
)在曲线上代入得λ=36.
所以双曲线C1的方程为: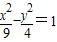 …(4分)
…(4分)
(2)由题意A1(-3,0),A2(3,0),Q(x,y).
当P异于顶点时,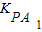 =
=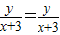 ,
,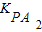 =
=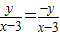
所以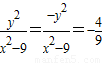 即
即 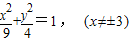 .
.
当P为顶点时直线PA1与 QA2的交点为顶点
所以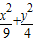 =1.…(9分)
=1.…(9分)
(3)设L交曲线C2于A(x1,y1),B(x2,y2),可设L方程为x=ty+1 (t≠0)
代入C2方程得 (9+4t2)y2+8ty-5=0
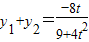 ,y1y2=
,y1y2=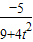 .
.
若存在N,则KAN+KBN=0 即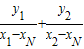 =0.
=0.
∴y1(ty2+1-xN)+y2(ty1+1-xN)=0
即 2t•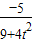 +(1-xN)•
+(1-xN)•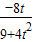 =0对t恒成立
=0对t恒成立
所以 xN=
故点N坐标为( ,0)…(14分)
,0)…(14分)
点评:本题主要考查直线与圆锥曲线的综合问题.解决这类问题的常用方法时,联立直线方程与圆锥曲线方程,再结合已知条件求解.
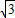 )在曲线上代入得λ=36即可得到结论;
)在曲线上代入得λ=36即可得到结论;(2)结合已知得到
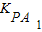 =
=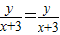 ,
,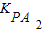 =
=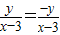 ;相乘整理即可得到结论;
;相乘整理即可得到结论;(3)先联立直线方程与曲线方程,得到
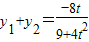 ,y1y2=
,y1y2=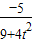 ;根据∠AKN=∠BKN得到KAN+KBN=0;整理后结合已知条件即可求出结论.
;根据∠AKN=∠BKN得到KAN+KBN=0;整理后结合已知条件即可求出结论.解答:解:(1)可设c1方程为 4x2-9y2=λ,又点(6,2
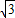 )在曲线上代入得λ=36.
)在曲线上代入得λ=36.所以双曲线C1的方程为:
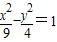 …(4分)
…(4分)(2)由题意A1(-3,0),A2(3,0),Q(x,y).
当P异于顶点时,
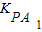 =
=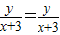 ,
,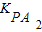 =
=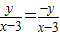
所以
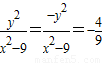 即
即 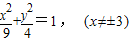 .
.当P为顶点时直线PA1与 QA2的交点为顶点
所以
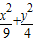 =1.…(9分)
=1.…(9分)(3)设L交曲线C2于A(x1,y1),B(x2,y2),可设L方程为x=ty+1 (t≠0)
代入C2方程得 (9+4t2)y2+8ty-5=0
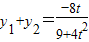 ,y1y2=
,y1y2=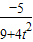 .
.若存在N,则KAN+KBN=0 即
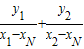 =0.
=0.∴y1(ty2+1-xN)+y2(ty1+1-xN)=0
即 2t•
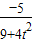 +(1-xN)•
+(1-xN)•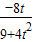 =0对t恒成立
=0对t恒成立所以 xN=

故点N坐标为(
 ,0)…(14分)
,0)…(14分)点评:本题主要考查直线与圆锥曲线的综合问题.解决这类问题的常用方法时,联立直线方程与圆锥曲线方程,再结合已知条件求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目